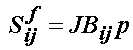I. Overview

       In the last section we introduced viscoelastic constitutive equations to model the time dependent stress-strain behavior of biologic tissues. In the case of viscoelasticity, the underlying physical mechanisms that give rise to the time dependent stress-strain behavior is not known. It is known that many biologic tissues are composed of porous solid matrices with fluid filling the pores. The overall mechanical behavior of these tissues depends not only on the solid matrix deformation, but also on the movement of the fluid in and out of the pores during the deformation. Since fluid plays a role in the load transfer in these tissues, it follows that the stress-strain behavior of these tissues will be time dependent. In fact, these fluid filled tissues often exhibit the same types of behavior including stress relaxation and creep that viscoelastic tissues exhibit. However, the mechanism for the creep and stress relaxation in fluid filled tissues is known, that of the fluid moving in and out of the solid matrix. This type of time dependent fluid-solid behavior is very prevalent for catilaginous tissues, although it is also known that blood vessels exhibit this fluid solid behavior. To model this behavior, parallel constitutive models have been developed, one denoted as poroelasticity and one as biphasic theory. Even though these theories developed from different roots, it can be shown that they are basically equivalent. In this section, we will outline the basic fundamentals of poroelasticity and biphasic theory as constitutive models of fluid filled solids.

II. Characteristics of a Poroelastic/Biphasic Material

      Just as viscoelastic materials exhibit time dependent response, so do biphasic/poroelastic models. In fact, the time dependent behavior of stress under a step strain and strain under a step stress is very similar to a viscoelastic material. Under a step strain, a poroelastic/biphasic material will undergo stress relaxation as shown below:

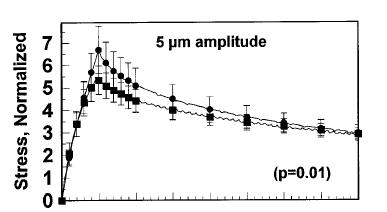
Under a step stress, a biphasic/poroelastic material will undergo creep, as shown in the case of articular cartilage below:

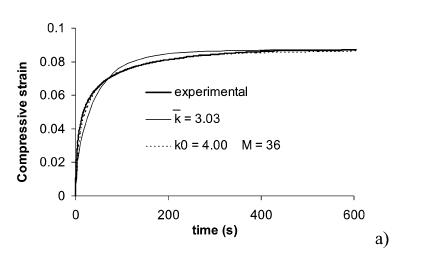
However, the underlying mechanism for creep/stress relaxation is different for a poroelastic/biphasic material versus a viscoelastic material. For a poroelastic/biphasic material, stress relaxation/creep come about due to the behavior of the fluid flowing relative to the solid. The governing equations for this behavior are described in the next section.

III. Linear Poroelastic and Biphasic Approaches

      To develop both the poroelastic and biphasic modeling approaches, we assume at a microstructural level that there is a mixture of a fluid/sold

We will describe the derivation first for poroelastic theory and then for biphasic theory. For poroelasticity, we describe the displacement of the solid in the typical manner as the position vector in the deformed configuration x minus the position vector in the reference configuration x':

The porosity of the material, that is, the volume of the pores divided by the total volume of the material is defined as:

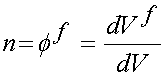
where n is the porosity, ff is the fluid volume fraction (the porosity is equivalent to the fluid volume fraction), dVf is the differential volume of fluid and dV is the total fluid volume. Biot, who originally described poroelasticity, defined a relative velocity between the fluid and solid part as:

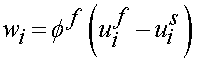
where wi is the relative displacement, uf is the fluid displacement, and other terms are as described previously. We can then write the governing stress equilibrium equation as:

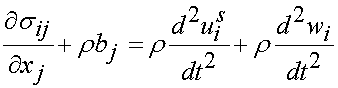
where sij is the Cauchy stress tensor, r is the solid density, wi is the relative displacement and the other terms are as defined preivously. Note that the above stress equilibrium equation is the same as that for a solid material, with the addition of a inertial force term due to the fluid. We also need a governing equation for the fluid phase, in terms of how the relative displacement of the fluid is related to the fluid pressure in the pores. It turns out that this is a well known phenomena and is modeled via Darcy's law, which in its generalized form is given below:

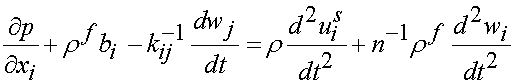
where p is the pore fluid pressure, kij is the permeability of the material, n-1 is the inverse of the porosity and the other terms are as defined previously. Thus, we now have two equations to solve for the governing behavior of the fluid and solid.

Once we have the governing equations, we can write the constitutive laws for a poroelastic material. For a compressible, anisotropic linear poroelastic material is:

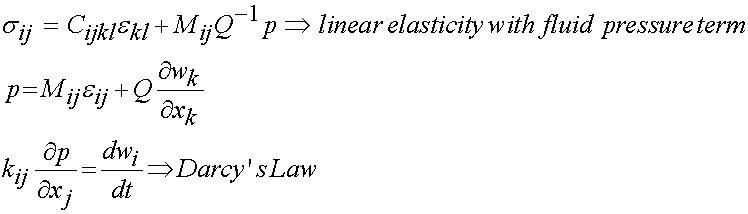
For the constitutive model given above, the total number of constants to be determined would be 34, 21 for Cijkl, 6 for Mij, 6 for kij, and 1 for Q. If the material is isotropic, then the above constitutive model reduces to:

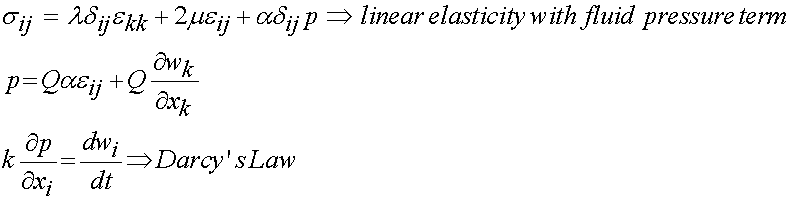
and there are 5 constants to determine: l, m, a, Q, and k.

Next, let us consider the linear biphasic theory. For biphasic theory, there are separate equilibrium problems for stresses in the solid:

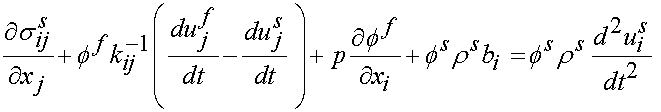
where all quantities with a super s denote solid and all quantities with a super f denote fluid, and the fluid:

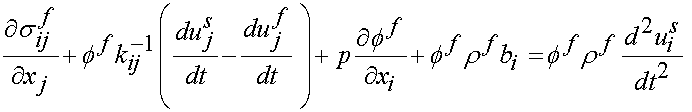
Note that the second term in both equilibrium equations represents a drag force due to the fluid slipping past the solid.

To see the equivalence, we can borrow a table from Simon (1992) for the linear poroelastic and biphasic theories:

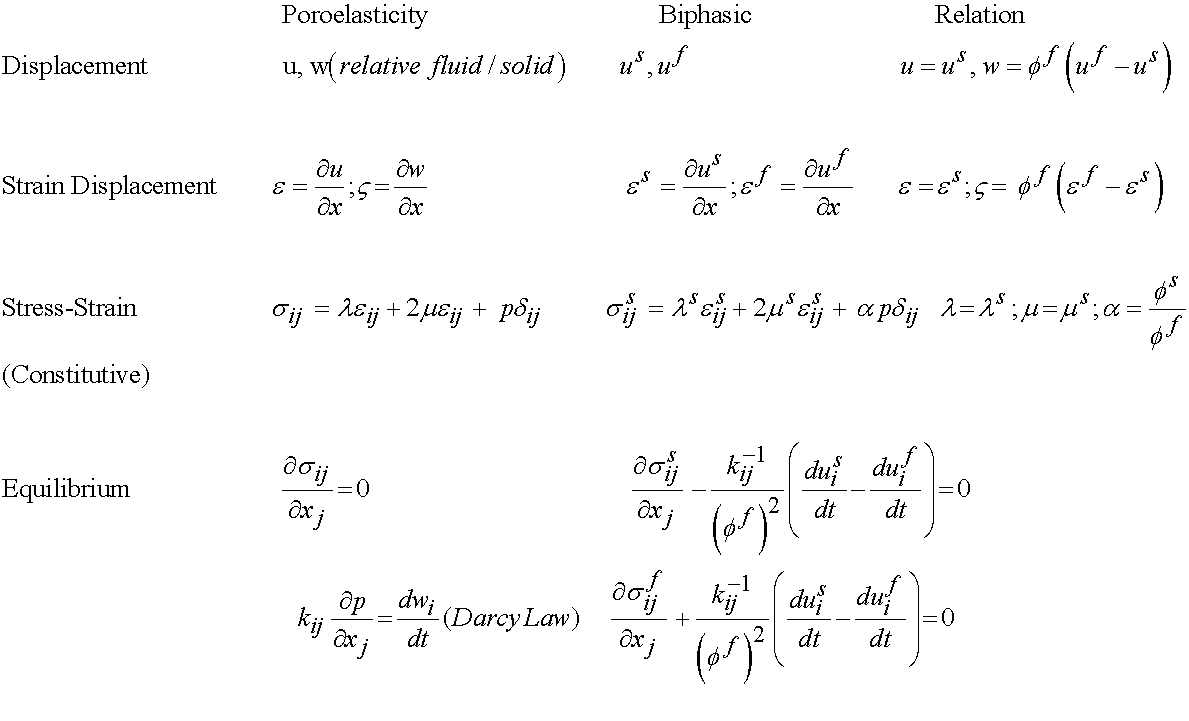IV. Poroelastic and Biphasic Approaches: Extension to Nonlinear Elastic Solid Matrix, Large Deformation

      To extend poroelasticity and biphasic theory to nonlinear materials, we can combine the strain energy functions used for nonlinear elastic materials with the fluid/solid approaches. Instead of using the linear elastic constitutive model, we instead use the strain energy functions commonly used for nonlinear elasticity modified to account for fluid pore pressure. An example of a porohyperelastic strain energy function given by Simon (1992) is:

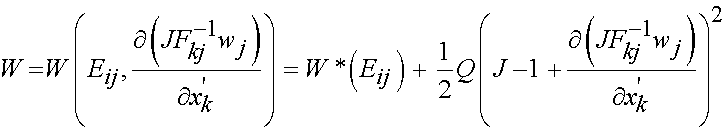
The term W* represents the energy due to elastic deformation and the second terms represents energy due to hydrostatic pressure in the fluid. To consider the last term, let us first note that the stress in the fluid in the deformed configuration, in other words, the Cauchy stress in the fluid is the hydrostatic pressure p. Thus, we know the Cauchy stress in the fluid as the hydrostatic pressure:

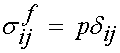
However, for the large deformation case, we need to write the fluid stress in terms of the 2nd PK stress. Recall the general formula for the transformation of the Cauchy stress to the 2nd PK stress:

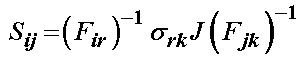
Thus, we have for the hydrostatic pressure:

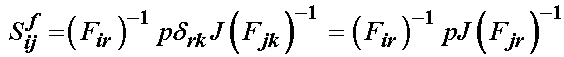
Many authors denote a special strain tensor denoted as Finger's strain tensor as:

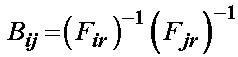
Thus, we can write the hydrostatic fluid pressure using Finger's strain tensor as:

Taking the energy function accounting for hydrostatic pressure, we can define a solid and fluid component to the 2nd PK stress as:

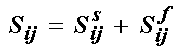
where Sf is the fluid hydrostatic pressure defined above, and Ss is the stress in the solid component defined as:

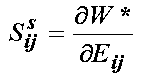
Here the strain energy function could use any of the forms defined in the nonlinear elasticity section. In addition, Simon proposed the following forms:

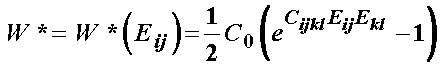
where the subsequent solid portion of the 2nd PK stress is derived as:

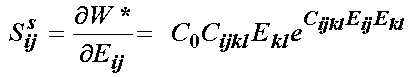
Simon also suggested familiar isotropic versions of the strain energy function as:

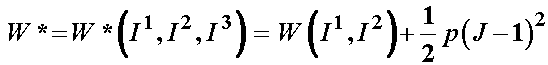
Finally, it is important to note that for a poroelastic/biphasic material undergoing large deformation that the permeability will depend on the deformation. This makes intuitive sense as one may expect that as the pores are deformed the permeability will change. To capture this behavior, Simon proposed the following deformation dependent permeability:

                                   

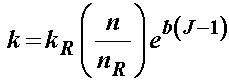
VI. Summary

       Poroelasticity/Biphasic theory is the third and final constitutive theory that will be reviewed in the class. As we have seen, it combines an elastic solid with pores that are filled with fluid. The interaction between the fluid and the solid determine the overall deformation behavior of the tissue. Poroelastic/biphasic theories are similar in basic concepts, although the exact field equations may differ. In addition to the elastic constants normally measured in a linear elastic or nonlinear elastic model, the permeability of the porous solid must also be measured.