
I. Introduction General Circulation models have predicted a two degree increase in global
temperatures by the end of the next century caused by an expected doubling
in atmospheric carbon dioxide (Jetten 1996). If global warming occurs,
increased temperatures may have tremendous implications for viral diseases
whose vectors are sensitive to climate changes. One disease implicated,
which is thought to pose the greatest threat in the case of global warming
in North America (Shope, 1991), is dengue fever. Dengue fever is transmitted
by Aedes aegypti, a vector whose rates of viral infection vary with climate
conditions (Reiter, 1988). It has been predicted that global warming may
shift the distribution and frequency of dengue, with dire consequences
to public health in the areas affected (Patz et al., 1996). To develop
a more accurate prediction of possible future scenarios, this study evaluated
retrospectively the relationship between morbidity incidence attributed
to dengue fever in Trinidad and Tobago and local variation in temperature
and precipitation. This study analyzed weekly dengue morbidity data from
the country of Trinidad and Tobago and monthly precipitation and temperature
data from the Port of Spain, Trinidad for a nine year period (1982-1990).
II. Objectives The main objective of this study was to determine retrospectively, whether
there was a temporal pattern of association between weather variables and
dengue fever morbidity rates. Because mosquito density, activity, and survival
is related to various weather conditions, there may be a correlation between
dengue incidence and weather patterns. However, it is uncertain whether
temperature or precipitation will be the strongest predictor of dengue
incidence, or whether a more predictive relationship exists when both are
taken into account. The time lag between weather patterns and possible
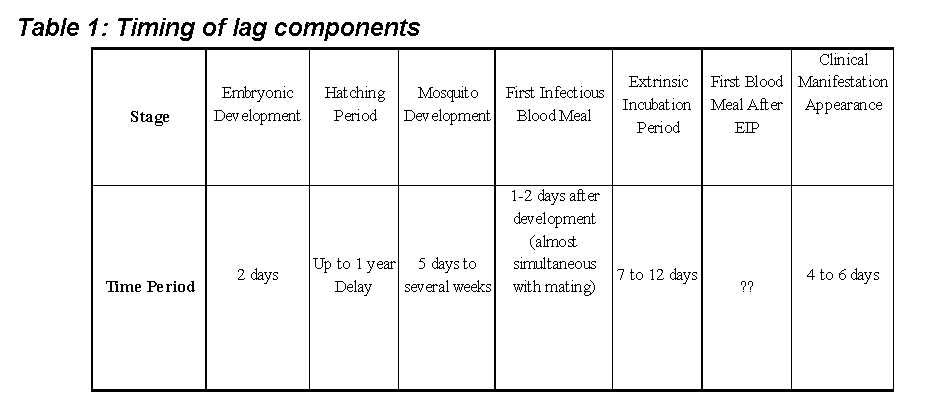
increases in dengue incidence is also uncertain. The various components
of the time lag include the period of embryonic development of the mosquito,
hatching time, the adult and sexual development period of the mosquito,
the time before the first blood meal, the extrinsic incubation period,
the time before the next blood meal in which the mosquito passes the infectious
virus, and the time before the appearance of clinical manifestations of
dengue fever (Table 1). It has been found that the development of the dengue
virus in the mosquito, the extrinsic incubation period (EIP), will range
from seven to twelve days depending on ambient temperature (Watts, 1987).
It has also been determined that the period between infection and clinical
manifestations of disease in humans ranges from four to six days (Pan American
Health Organization, 1994). It is therefore assumed that a time lag of
at least eleven and perhaps as much as eighteen days will be found. However
this may be a very conservative estimate as it does not take into account
the life cycle and development of the mosquito which varies according to
ambient weather conditions, the availability of food , and larval density
in the container in which the mosquito is breeding. Hatching of the mosquito
varies dramatically according to precipitation and humidity; a dry period
may mean the mosquitoes will delay hatching for more than a year (Pan American
Health Organization, 1994). The delayed development could potentially provide
a much greater time lag than expected, possibly a time lag of greater than
a year. However, because such long dry periods do not occur in Trinidad,
a time lag of less than one year is more likely. The goal of this effort
was to evaluate whether a temporal association, possibly with a time lag,
exists between weather variables and disease incidence.
III. Background Dengue fever is caused by a virus from the family Flavviviridae; four
serotypes are distinguished by serological methods, dengue-1, dengue-2,
dengue-3, and dengue-4. All four serotypes have been found in the Americas,
however only serotypes 1, 2, and 4 circulated in the period focused on
for this study (1982-1990). The virus is transmitted primarily by the Ae.
aegypti mosquito to the human host. Ae. aegypti is a highly domesticated
mosquito, breeding in freshwater containers stored for drinking and bathing.
Because severe frost and cold weather kills adult mosquitoes and eggs,
dengue is currently restricted to the region between thirty-five degrees
north latitude and thirty-five degrees south latitude. The clinical manifestations
of dengue can range from a minor fever, often with flu-like symptoms, to
severe Dengue Hemorrhagic Fever (DHF) and Dengue Shock Syndrome (DSS) that
may result in death. Between 250,000-500,000 cases of the severe DHF/DSS
form occur yearly throughout the world and case fatalities can reach forty
to fifty percent if not treated with fluid replacement therapy (Gubler,
1994). The relationship between weather patterns and dengue transmission
is multifaceted involving both the mosquito life cycle and viral replication
requirements. It has been determined that warmer temperatures reduce larval
size of Ae. aegypti which results in a smaller adult size (Rueda, 1990).
Smaller adult female mosquitoes have been found to feed more frequently
to nourish their developing eggs (Reiter, 1988) which increases the probability
of transmission. The positive relationship between biting rates and temperature
has been supported in field studies in Bangkok (Pant, 1973). A second consideration
in viral transmission is the EIP. A study by Watts et al. (1987) determined
that the EIP is heavily contingent upon temperature; the EIP for Ae. aegypti
decreased from twelve to seven days when mosquitoes were kept at 32-35
degrees instead of 30 degrees Celsius. These results imply temperature
induced variations in the vectorial efficiency of Ae. aegypti may be a
significant determinant of the annual pattern of dengue that Watts et.
al. found in Bangkok. Research by Koopman et al. (1991) also supports the
theory that dengue transmission frequency relies upon climatic conditions.
His study concluded that median temperature during the rainy season was
the strongest predictor of infection. High temperature was responsible
for greater transmission rates by reducing the period of viral replication
in mosquitoes. It has been found that increasing precipitation may either
increase or decrease dengue incidence rates. It has been proposed that
human vector contact may be enhanced during periods of high rainfall (Gubler,
1994) because mosquitoes may become less active. In this scenario they
are more likely to stay indoors where their probability of survival is
higher and their contact with humans is greater. However, many scientists
have found an inverse relationship between incidence rates and rainfall.
In his 1938 study, Soper found that low rainfall in Brazil results in more
water storage containers in the home and therefore more Ae. aegypti in
residential areas. The implications of global warming on dengue transmission
has been modeled by Martens et. al. (1997) who found that the transmission
potential of dengue may be highly sensitive to climate changes. They predicted
that transmission should be particularly sensitive to warming in higher
altitudes and in areas which are currently at the periphery of endemic
transmission. Jetten and Focks (1996) have also developed a model of the
influence of warming on the intensity and distribution of dengue throughout
the world. Using a simulation model projection, their results indicate
that the current warming prediction of two degrees by 2100 may result in
an increase in the latitude and altitude range of dengue. They also concluded
that the duration of the transmission season could increase in temperate
locations. As yet, there has been no study published of actual case data
that seeks a retrospective statistical association between weather variables
and dengue incidence. Studies of dengue in the past have not looked at
weather factors independently, nor have they looked longitudinally at how
these factors may affect morbidity rates. My study is intended to evaluate
the relative importance of temperature and precipitation rates to transmission
using long-term case data from the islands of Trinidad and Tobago.
IV. Data Monthly mean precipitation and temperature data were collected from
the Web Page of the National Climatic Data Center (http://www.ncdc.noaa.gov/ghcn/ghcn.html).
While Tobago did have its own weather station located at Crown Point Airport,
this data was unavailable therefore all weather information came from the
Piarco International Airport in Trinidad. The mean temperature and precipitation
were used, as opposed to either the minimum or maximum temperature, because
it has been found that incidence rates of malaria are most closely related
to mean temperature at lower altitudes (Loevinsohn, 1994). Because the
disease etiology of malaria is somewhat similar to that of dengue (they
are both diseases carried by mosquitoes whose living and breeding conditions
are contingent upon the ambient environment) and because Trinidad is at
an elevation of twelve meters, I chose the mean temperature and precipitation
values. However, it is important to note that malaria and dengue are differentiated
by difference species of mosquito vectors, entirely different infectious
parasites, and different patterns of breeding and development of the vectors.
Therefore, it is possible that minimum and maximum temperatures may be
useful in predicting a relationship between weather variables and morbidity
rates. The weekly incidence rates of dengue in Trinidad and Tobago were
obtained from Dr. Wilson of the University of Michigan Department of Epidemiology.
Because data from Trinidad alone was unavailable, I used the coalesced
data which included morbidity from both Trinidad and Tobago. The weekly
rates were converted to monthly rates, assuming that whatever fraction
of the week was ascribed to one of two months, if it was a week split between
two months, a similar proportion of incidence was given.
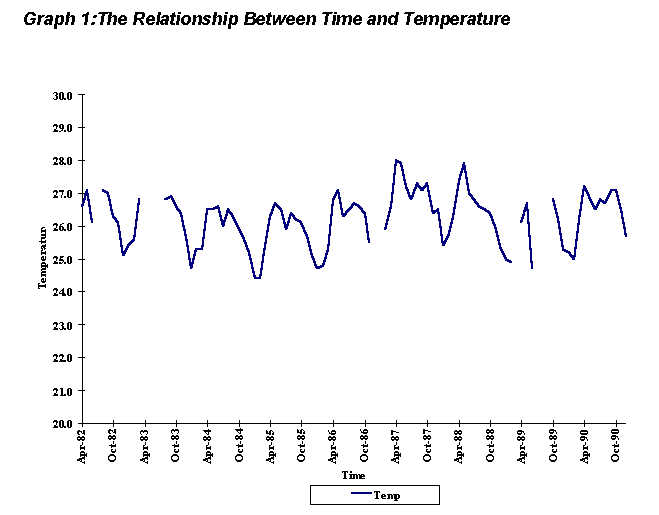
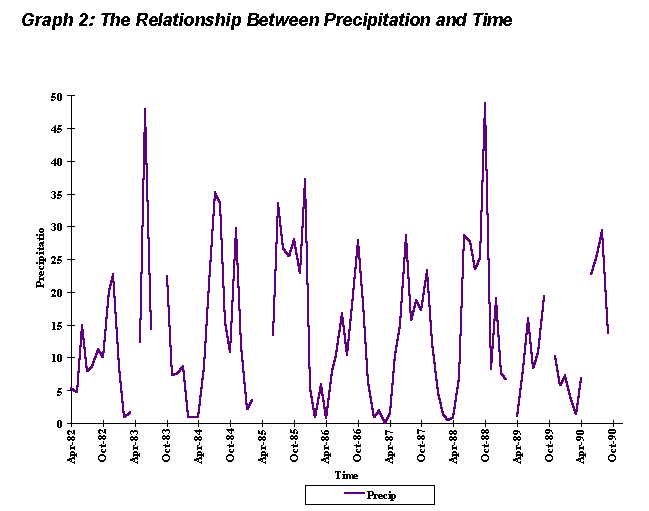
V. Qualitative Description of the data The nine year period of monthly temperature data varied less that 4
degrees Celsius. A seasonal distribution of maximum and minimum temperatures
exists; annual maximum temperatures were usually observed in the months
of May through September, and annual minimum temperatures were found in
either December or January (Graph 1).
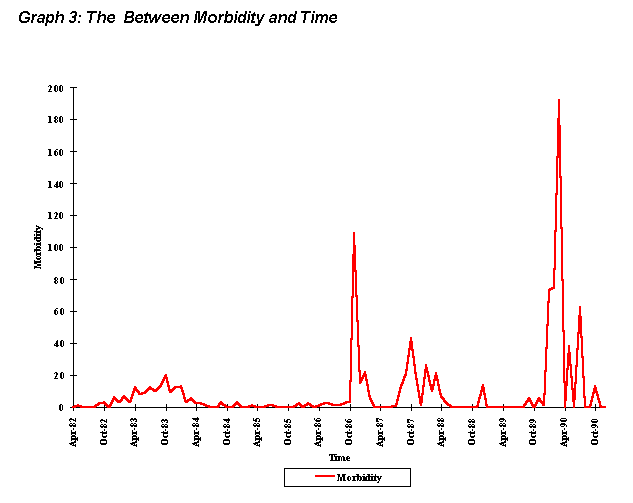
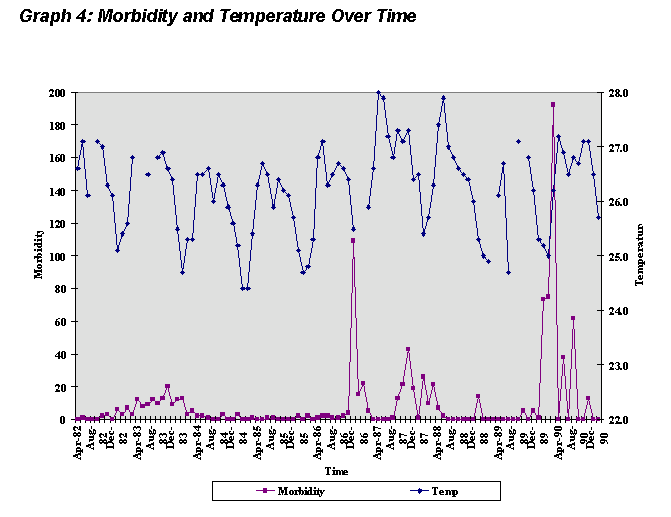
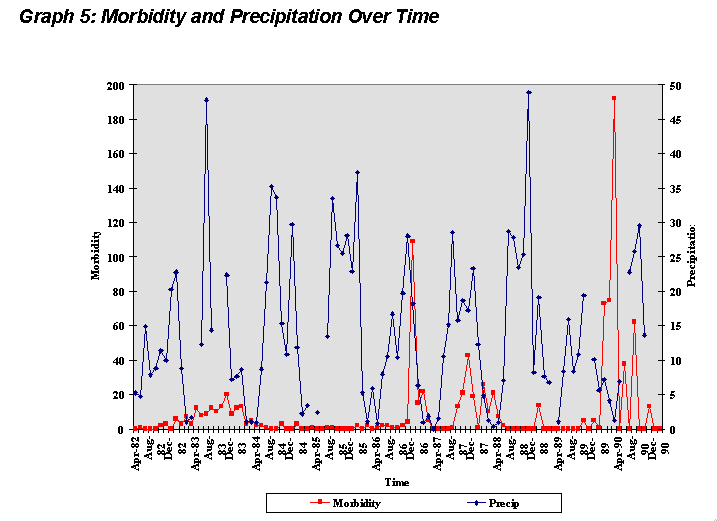
VI. Methods/Approach To determine the most appropriate model to demonstrate the possible
relationship between morbidity due to dengue fever weather variables, several
approaches were undertaken (Thesis1-Thesis 3). Thesis 1: Four separate
models were tested to determine the most appropriate one: a linear model,
an exponential growth model, an autoregressive model with a time lag of
one month, and an exponential growth autoregressive model with a time lag
of one month. I conjectured that the relationship between the variables
may not be linear and thought it best to try both the linear and exponential
models with a time lag of one month. To determine the most appropriate
model, a regression was run for each of the situations to find the amount
of error explained by each model. Also to determine the robustness of the
models, the F statistics were calculated, as were their corresponding p-value.
Because one of the assumptions of multiple regressions is that errors of
the variables are not related to one another, the Durbin Watson statistic
was calculated to determine possible serial-correlation. To test the null
hypothesis that neither precipitation nor temperature were related to morbidity
rates, the t-statistic was calculated with its corresponding p-value. Finally,
an equation for the line of each model was determined. Results of Thesis
1: The results of the four models showed no statistical significance for
each model, nor were any of the variables alone statistically significant.
The Durbin Watson statistic indicated that there was serial correlation
between the variables as might be expected between temperature and precipitation
which often affect one another. Because a linear relationship with time
lags is more likely than an exponential relationship, I chose to retain
the linear model for the remainder of the tests. Thesis 1a: To determine
whether a better model might be achieved if the outliers were removed,
the previous four models were tested after removing monthly records in
which either the morbidity was greater that 50 or the precipitation was
greater than 30. Because there were no outliers for temperature, no temperature
records were removed. Results of Thesis 1a: The results of the four models
with the outliers excluded showed no statistical significance for each
model, nor were any of the variables alone statistically significant. The
Durbin Watson statistic indicated that there was serial correlation between
temperature and precipitation. Thesis 2: The linear model was retained
because although no statistically significant relationship exists without
a time lag or a time lag of only one month, a likely relationship may exist
with a time lag of up to one year. To determine if such a relationship
is a possibility, the dependent variable was lagged against the two weather
variables by each month for up to twenty-four months. Results of Thesis
2: Several statistically significant relationships were found during this
test. First, the model with a time lag of six months was statistically
significant with an F statistic equal to 3.935, corresponding to a p-value
of .0234. To reject the null hypothesis that there was no statistically
significant relationship between incidence and the weather variables, the
p-value had to be .05 or less. The R-squared value was .0889 which indicates
that 8.89 percent of the error is explained by the model. Temperature,
with a t-value of 2.64 corresponding to a p-value of .0098, was statistically
significant, while precipitation was not a statistically significant parameter.
To reject the null hypothesis, that there was no statistically significant
relationship between temperature or precipitation and incidence, the t-values
for either of the weather variables had to be greater than 1.96 with a
corresponding p value of .05 or less. The correlation between temperature
and precipitation was positive, with a value of .2504, and the correlation
between precipitation and temperature was negative with a correlation value
of -.0239. The Durbin Watson statistic indicated that serial-correlation
between the two independent variables was occurring and had a value of
1.735 ( a value of 2 indicates that there is no serial correlation). The
equation for this model is -142.26 = 5.83 Beta 1 - .196 Beta 2 + error
term. The other two statistically significant models were at lags of thirteen
and seventeen months, which is too long a period to represent an actual
relationship and is likely an artifact of lagging the model for too many
months. Because long periods of desiccation do not occur in Trinidad, it
is most probable that the existing lag is less than one year. Neither of
the models were more statistically significant than the model with the
six month lag. At the lag of 6 months the F value was 3.211 with a corresponding
p-value of .0459. The R-squared value was .0789 indicating that 7.89 percent
of the error is explained by the model. Temperature, the only statistically
significant variable for this model, had a t-value of -2.52 with a corresponding
p-value of .01. In this model, temperature was negatively correlated with
morbidity with a correlation of -.279 and precipitation was positively
correlated with morbidity with a correlation of .0197. The equation for
this model is 261.81 = -9.963 Beta 1 + .1098 Beta 2 + error term. The other
model with a statistically significant relationship which is likely an
artifact of lagging for too many moths is found at 17 months. The F value
for this model was 4.059 with a corresponding p-value of .02. The R-squared
value was .1001 indicating that 10.01 percent of the error is explained
by the model. Precipitation, the only statistically significant variable
in this model, had a t-value of 2.77 with a corresponding p-value of .007.
Precipitation was positively correlated with morbidity with a correlation
of .319 and temperature was positively correlated with morbidity with a
correlation of .065 in this model. The equation for this model is -39.36
= 1.53 Beta 1 + .76 Beta 2 + error term. Thesis 2a: To test whether temperature
as the only independent variable would create a better model, regressions
were run of temperature against morbidity lagging the variables up to twenty-four
months. Results of Thesis 2a: Two statistically significant relationships
were determined. At a lag of six months, the model was statistically significant
with an F statistic of 5.887 and a corresponding p-value of .0173. The
R-squared value was .0627 which indicates that 6.27 percent of the error
is explained by the model. The t-value was 2.426 with a corresponding p-value
of .0173, indicating that the variable is statistically significant. A
positive correlation between temperature and morbidity was found with a
correlation value of .2504. The equation for this model is -96.67 = 4.05
Beta 1 + error term. The second statistically significant relationship
was found at a time lag of thirteen months which, as explained previously
is too long a period to represent an actual relationship and is likely
an artifact of lagging the model for too many months. In this regression,
the F statistic was 6.84 with a corresponding p-value of .0106. The R-squared
was .0779 indicating that 7.79 percent of the error is explained by the
model. The t-statistic was -2.616 with a corresponding p-value of .0106.
There was a negative correlation between precipitation and morbidity with
a correlation value of -.279. The equation for the line is 257.24 = -9.4
Beta 1 + error term. Thesis 2b: To test whether precipitation as the only
independent variable would create a better model, regressions were run
of precipitation against morbidity lagging the variables up to twenty-four
months. Results of Thesis 2b: There was one statistically significant relationship
between precipitation and morbidity at a time lag of seventeen months.
However, this is likely an artifact of lagging the variables for too many
months. In this regression, the F statistic was 9.047 with a corresponding
p-value of .0036. The R-squared was .1016 indicating that 10.16 percent
of the error is explained by the model. The t-statistic was 2.008 with
a corresponding p-value of .0035. There was a positive correlation between
precipitation and morbidity with a correlation value of .318. The equation
for the line is .21 = .778 Beta 1 + error term. Thesis 3: Because it is
possible that precipitation and temperature have different time lags when
affecting morbidity, two models were tested using both independent variables
at different time lags. Because the time lags for temperature of six and
thirteen months and the time lag for precipitation of seventeen months
were statistically significant, the models used first a lag of six months
for temperature and seventeen months for precipitation, and then a lag
of thirteen months for temperature and seventeen months for precipitation.
Results of Thesis 3: Neither the model nor the independent variables were
statistically significant for both models tested. The Durbin Watson statistic
indicated that serial correlation was occurring between the variables.
These results suggest that either the variables are interacting with one
another or the time lags chosen are too great to indicate a real relationship.
VII. Equations for Each Model Thesis 1: Full dataset
There are two models which show the greatest likely relationship between
weather variables and morbidity due to dengue fever. Both of the models
at a time lag of six months, with temperature alone and with precipitation
and temperature together, were statistically significant and appear to
be the best models. The model did not greatly improve when temperature
was considered alone, therefore both models are considered appropriate
in explaining the association between morbidity and weather. Because the
time lag is six months, it suggests a seasonal relationship which may be
discerned through further research. As yet, my work has some errors which
can be overcome with more data and more time. It is possible that although
there were one hundred and eight data points and a minimum of twenty data
points is necessary for a statistically significant relationship to be
found, more data points are needed. Errors could also have been due to
the fact that the weather data was from Trinidad alone while the incidence
data was from both Trinidad and Tobago. It is possible that the weather
in Trinidad is not reflective of that in Tobago. Also, the method of changing
weekly incidence data to monthly incidence data may have induced errors.
It is likely that although a certain fraction of a week belongs to one
month, the corresponding fraction of incidence does not also belong to
that month. For example, there may be an outbreak in one month and not
the next, which would mean an unequal division of incidence for a week
split between those two months. Lastly, the small amount of serial correlation
between temperature and precipitation indicate that these two variables
are affecting one another which may reduce the robustness of the model.
To correct some of these problems a longer period of time should be analyzed,
the data should be given in monthly form for all variables, and all data
should be given from one locale. Also, using the minimum and maximum temperatures
in place of mean temperature may reveal a more predictive relationship. IX. Conclusions The statistical procedures suggest that there is a statistically significant
relationship between temperature and incidence rates given a six month
time lag. The results indicate that it takes six months for environmental
conditions, as measured by temperature alone, to affect dengue incidence.
This may be due to temperature’s influence on the life cycle of a mosquito
or viral replication rates. The higher temperatures may reduce the larval
size of mosquitoes, which results in smaller adults that need to feed more
often. Higher temperatures may also speed up the EIP causing greater rates
of transmission. Because the time lag for these to occur is nebulous due
to the variable nature to the mosquito life cycle, it difficult to verify
how these factors can be ascribed to the six-month time lag found. A small
negative correlation of precipitation with incidence was detected, suggesting
that precipitation six months prior to reporting dengue may reduce incidence
rates. This may be due to a variety of factors. Either high amounts of
rain flush out larvae, thereby reducing rates or low amounts of rain requires
more water to be stored which will increase incidence rates. In either
situation an inverse relationship is observed between precipitation and
incidence rates. However, because no statistically significant relationship
of precipitation with incidence was found, precipitation did not actually
influence incidence, only a negative correlation between the two variables
can be alluded to. X. Public Health Implications Because this study indicates that there is a statistically significant
relationship between dengue incidence and temperature at a six month time
lag, there are both present and future public health implications. The
present implications of this study suggest that disease prevention and
surveillance measures should focus on the temperature six months prior
to determine the risks of increased transmission for the present time.
The future implications of this study are more uncertain. Because a positive
correlation of temperature with incidence was found, global warming is
likely to have an impact on dengue fever, increasing the disease’s range
and the number of infected individuals. To mitigate future impacts both
disease surveillance and control are necessary. Disease surveillance should
include both passive and active surveillance. Passive surveillance would
require dengue be a mandated reportable disease that would be recorded
in all hospitals and clinics. Active surveillance includes providing a
laboratory-based surveillance system which would give public health officials
precise information about periods of increased dengue activity. One active
surveillance measure suggested is the creation of diagnostic centers in
sensitive geographic regions bordering endemic zones (Patz et al., 1996).
Such centers would provide early warning of changes in incidence and allow
for intervention. Control measures should have an integrated approach combining
environmental management, chemical control, and biological methods. Environmental
management is any change in the environment that prevents or minimizes
vector propagation or man-vector-pathogen contact. These include environmental
modification (long-term changes to vector habitat such as improved delivery
of potable water), environmental manipulation (short-term changes to vector
habitat including proper storage of containers), and changes to human habitation
or behavior (including the screening of windows). Chemical control should
be used in a limited fashion because of the toxic effects most larvicides
have had to humans and aquatic organisms in the past. Present use is restricted
to containers that cannot otherwise be eliminated or managed. Biological
control is based on the introduction of living organisms that will prey
upon, parasitize, compete with or otherwise reduce the abundance of Aedes
or anopheline mosquitoes. These interventions have been largely experimental
and have included introduction of fish, bacteria, and cylclopoids (‘water
fleas") which attempt to reduce mosquito populations. If little is done
to prevent global warming, surveillance and control measures will be our
last protection against increasing infectious disease transmission. However,
preventing warming should be a greater priority to ensure that global dissemination
of communicable diseases does not occur.
References
Thesis 1a: Deleting observations where Morbidity > 50 and Precipitation
> 30
MORBID = alpha + (Beta1)(Temp) + (Beta2)(Precip) + error term
log(MORBID) = alpha + (Beta1)(Temp) + (Beta2)(Precip) + error term
MORBIDt = alpha + (Beta1)(Tempt-1) + (Beta2)(Precipt-1) + error term
log(MORBIDt )= alpha + (Beta1)[log(Tempt-1)] + (Beta2)[log(Precip t-1)]
+ error term
Thesis 2: Full dataset
MORBID = alpha + (Beta1)(Temp) + (Beta2)(Precip) + error term
log(MORBID) = alpha + (Beta1)(Temp) + (Beta2)(Precip) + error term
MORBIDt = alpha + (Beta1)(Tempt-1) + (Beta2)(Precip t-1) + error term
log(MORBIDt )= alpha + (Beta1)[log(Tempt-1)] + (Beta2)[log(Precip t-1)]
+ error term
Thesis 2a: Full dataset
MORBIDt = alpha + (Beta1)(Tempt-1) + (Beta2)(Precip t-1) + error term
Thesis 2b: Full dataset
MORBIDt = alpha + (Beta2)(Temp t-1) + error term
Thesis 3: Full dataset
MORBIDt = alpha + (Beta1)(Precipt-1) + error term
VIII. Discussion
MORBIDt = alpha + (Beta1)(Temp t-1) + (Beta2)(Precipt-1) + error term