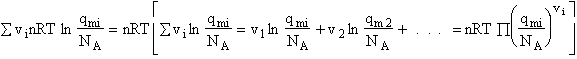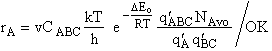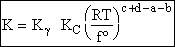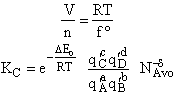Professional Reference Shelf
R3.2 Transition State Theory
Abbreviated Lecture Notes
Transition State Theory
Full Lecture Notes
- Overview
-
Introduction
- The Transition State
- Procedure to Calculate the Frequency Factor
-
Background
- Molecular Partition Function
- Relating , ni and N
- Relate and q
- Canonical Partition Function for Interacting Molecules
- Thermodynamic relationships to relate , and q
- Relate G, the molar partition function qm
- Relating the dimensionless equilibrium constant K and the molar partition function
qm
- Relate the molecular partition function on a basis of per unit volume, q' and the
equilibrium constant K
- Recall the relationship between K and KC from Appendix C.
- The Loose Vibration, vI
- Evaluating the Partition Functions
- The Eyring Equation
- Problems
I. Overview
|
Transition state theory provides an approach to
explain the temperature and concentration dependence of the rate law. For example, for the elementary reaction
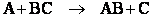
The rate law is
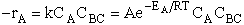
For simple reactions transition state can predict E and A in concert with computational chemistry. In transition
state theory (TST) an activated molecule is formed during the reaction at the transition state between forming
products from reactants.
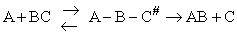
The rate of reaction is equal to the product of the frequency, vI, of the
activated complex crossing the barrier and the concentration of the transition state complex
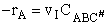
The transition state molecule 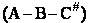 and the reactants are in
pseudo equilibrium at the top of the energy barrier. and the reactants are in
pseudo equilibrium at the top of the energy barrier.
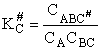
Combining
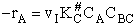
We will now use statistical and quantum mechanics to evaluate 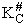 to arrive at the equation to arrive at the equation
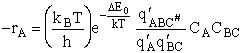
where q¢ is overall the partition function per unit volume and is the product of
translational, vibration, rotational and electric partition functions, i.e.,
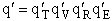
The individual partition functions to be evaluated are:
Translation
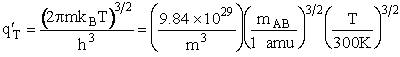
Vibration
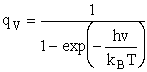
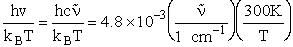
Rotation
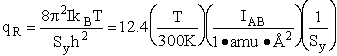
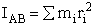
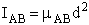 for diatomic molecules for diatomic molecules
The Eyring Equation
Liquids
Gases
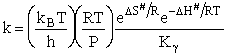
|
R. I. Masel, Chemical Kinetics and Catalysis, Wiley Interscience, New York, 2001.
References Nomenclature
A5p403 Means Atkins, P. W. Physical Chemistry, 5th ed. (1994) page 403.
A6p701 Means Atkins, P. W. Physical Chemistry, 6th ed. (1998) page 701.
L3p208 Means Laidler, K. J., Chemical Kinetics, 3rd ed. (1987) page 208.
M1p304 Means Masel, R.I., 1st Edition (2001) page 304.
II. Introduction
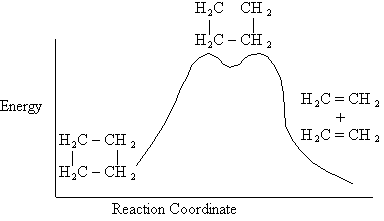
Figure PRS.3B-1 Evidence of Active
Intermediate.
The active intermediate is shown in transition state at the top of the energy barrier. A
class of reactions that also goes through a transition state is the SN2
reaction.
A. The Transition State
We shall first consider SN2 reactions
[Substitution, Nucleophilic, 2nd order] because many of these reactions can be described by
transition state theory. A Nucleophile is a substance (species) with an unshared electron. It is a species that seeks
a positive center.

, i.e.,

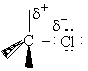
The nucleophile seeks the carbon atom that contains the halogen. The nucleophile always approaches from the
backside, directly opposite the leaving group. As the nucleophile approaches the orbital that contains the
nucleophile electron pairs, it begins to overlap the empty antibonding orbital of the carbon atom bearing the leaving
group (Solomon, T.W.G, Organic Chemistry, 6/e Wiley 1996, p.233).
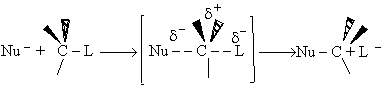

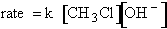
The Figure PRS.3B-1 shows the energy of the molecules along the reaction coordinate which measures the progress of
the reaction. [See PRS.A Collision theory-D Polyani Equations]. One measure of this progress might be the distance
between the CH3 group and the Cl atom.


Figure PRS.3B-2 Reaction
coordinate for (a) SN2 reaction, and (b) generalized
reaction
Collision Theory when discussing the Polyani Equation.
The energy barrier shown in Figure PRS.3B-2 is
the shallowest barrier along the reaction coordinate. The entire energy diagram for the ABC system is
shown in 3-D in Figure PRS.3B-3. To obtain Figure PRS.3B-2 from Figure PRS.3B-3 we start from the initial state
(A + BC) and move through the valley up over the barrier, Eb, (which is also in a valley) over
to the valley on the other side of the barrier to the final state (A + BC). If we plot the energy along the
dashed line pathway through the valley of Figure PRS.3B-3 we arrive at Figure PRS.3B-2.
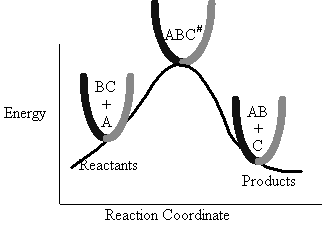
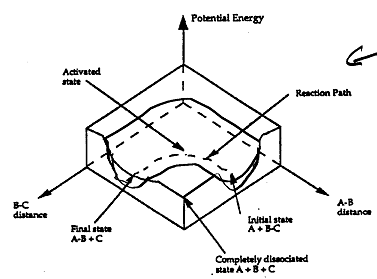
Figure PRS.3B-3 3-D energy surface
for generalized reaction.
The rate of reaction for the general reaction (Lp90) is the rate of crossing the energy barrier
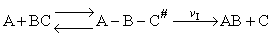
We consider the dissociation of the activated complex 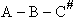 as a loose vibration of frequency vI, (s1). The rate of crossing the energy barrier is just
the vibrational frequency, vI, times the concentration of the activated
complex,
as a loose vibration of frequency vI, (s1). The rate of crossing the energy barrier is just
the vibrational frequency, vI, times the concentration of the activated
complex, 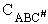
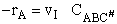 (1)
(1)
We assume the activated complex ABC# is in virtual equilibrium with the
reactants A and BC so we can use the equilibrium concentration constant 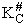 to relate these concentrations, i.e.,
to relate these concentrations, i.e.,
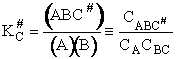 (2)
(2)
Combining Eqns. (A) and (B) we obtain
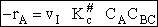 (3)
(3)
The procedure to evaluate vI and 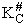 is shown in the table T.S.1
is shown in the table T.S.1
B. Procedure to Calculate the Frequency Factor
Table PRS.3B-1 Transition State Procedure to Calculate vI
and 
Step 1)A. Molecular partition function. The number of ways, W,
of arranging N molecules in m energy states, with ni molecules in the
ei energy state is

The distribution that gives a maximum in W is the Boltzmann distribution from which we obtain the molecular
partition function, q.
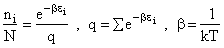
Step 2)B. Relating  , ni and
N.
, ni and
N.
The entropy or the system is given by the fundamental postulate
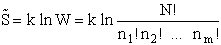
Next we manipulate the Boltzmann equation for N molecules distributed in m energy states using Stirling's
approximation to arrive at

Step 3)C. Relate  and q. Starting with the total energy of the system
E=
and q. Starting with the total energy of the system
E=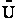
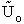 =
=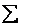 niei, relative to the ground state, substitute for the number of
molecules, ni, in energy state eI, using the Boltzmann distribution in the last equation of Step 3
niei, relative to the ground state, substitute for the number of
molecules, ni, in energy state eI, using the Boltzmann distribution in the last equation of Step 3
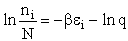
and then sum to arrive at
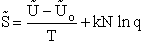
for non-interacting molecules. 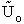 is the ground state
energy.
is the ground state
energy.
Step 4)D. Canonical partition function for interacting
molecules. We need to consider interacting molecules and to do this we have to use Canonical partition
function
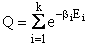
with the probability of finding a system with energy Ei is
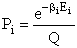
These relationships are developed with the same procedure as that used for the molecular partition function. For
indistinguishable molecules, the canonical and molecular partition functions are related by
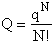
using the above equation we can arrive at
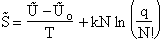
Step 5)E. Thermodynamic relationship to relate
 ,
, 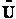 and qi, the
molecular partition function
and qi, the
molecular partition function
We begin by combining the Maxwell relationship, i.e.,
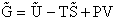
with the last equation in Step 4 where the tilde (e.g. 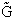 )
represents the symbols are in units of kcal or kJ without the tilde is in units per mole, e.g., kJ/mol. We first
use the last equation for S in Step 4 to substitute in the Maxwell Eqn. We next use the relationship between Q and
q, i.e.,
)
represents the symbols are in units of kcal or kJ without the tilde is in units per mole, e.g., kJ/mol. We first
use the last equation for S in Step 4 to substitute in the Maxwell Eqn. We next use the relationship between Q and
q, i.e.,
To relate 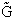 to q, the molecular partition function.
For N indistinguishable molecules of an ideal gas
to q, the molecular partition function.
For N indistinguishable molecules of an ideal gas
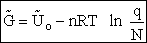
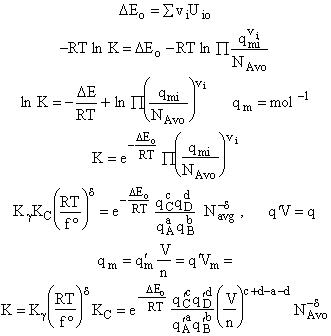
Step 6)F. Relate G to the molar partition function
qm. We define qm
as
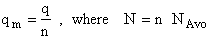
and then substitute in the last equation in Step 5.
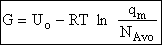
Note: The tilde's have been removed.
where n = Number of moles, and NAvo = Avogadro's number and where G and
Uo are on a per mole basis, e.g. (kJ/mole).
Step 7)G. Relate the dimensionless equilibrium constant K and the molar
partition function qmi
For the reaction
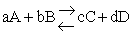
the change in the Gibb's free energies is related to K by
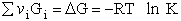

Combining the last equation in Step 6 and the above equations
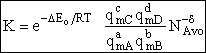
where
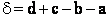
Step 8)H. Relate the partition function on a per unit volume basis,
q¢, and the equilibrium constant K
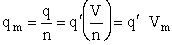
Where Vm is the molar volume (dm3/mol).
Substituting for qmi in the equation for K in Step 7 we obtain
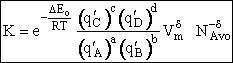
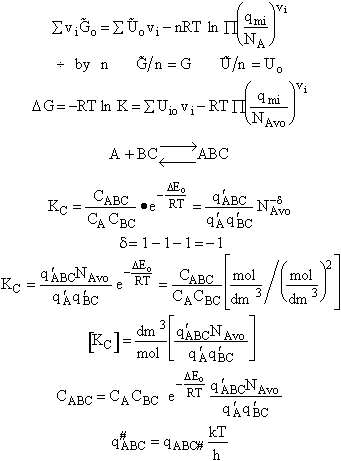
Step 9)I. Recall the relationship between K and
KC from Appendix C
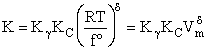
Equate the equilibrium constant K given in the last equation of Step 8 to the thermodynamic K for an ideal gas,
( ) to obtain KC in
terms the partition functions, i.e.,
) to obtain KC in
terms the partition functions, i.e.,
For the transition state A B C#, with d = 1,
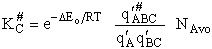
we also know
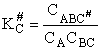
Equating the two equations and solving for 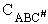
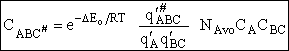
The prime, e.g., q', denotes the partition functions are per unit volume.
Step 10) J. The loose
vibration.
The rate of reaction is the frequency, vI, of crossing the barrier times the
concentration of the activated complex 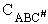

This frequency of crossing is referred to as a loose (imaginary) vibration. Expand the vibrational partition
function to factor out the partition function for the crossing frequency.
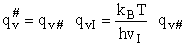
Note that # has moved from a superscript to a subscript to denote the imaginary frequency of crossing the barrier
has been factored out of both the vibrational, 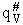 and
overall partition functions, q#, of the activated complex.
and
overall partition functions, q#, of the activated complex.
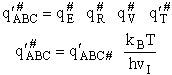
Combine with rate equation, 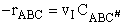 noting that vI cancels out, we obtain
noting that vI cancels out, we obtain

where A is the frequency factor.
Step 11) K. Evaluate the partition functions
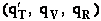
Evaluate the molecular partition functions.
Using the Schrödenger Equation
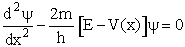
we can solve for the partition function for a particle in a box, a harmonic oscillator and a rigid rotator to
obtain the following partition functions
Translation:
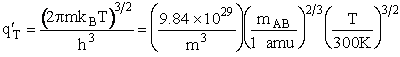
Vibration:
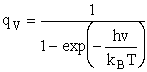
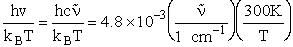
Rotation:
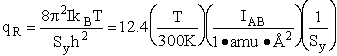
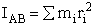
The end result is to
evaluate the rate constant and the activation energy in the equation

We can use computational software packages such as Cerius2 or Spartan to calculate the partition functions of the transition state and to get the
vibrational frequencies of the reactant and product molecules. To calculate the activation energy one can either use
the barrier height as EA or use the Polyani Equation.

III. Background
A. Molecular Partition Function
In this section we will develop and discuss the molecular partition function for N molecules with a fixed total
energy E in which molecules can occupy different energy states, ei.
Total Energy of System
Total number of molecules, N,
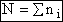 (4)
(4)
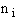 = Number of molecules with energy ei
= Number of molecules with energy ei
The total Energy E is
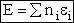 (5)
(5)
The number of ways, W, arranging N molecules among m energy states (e1, e2 . . . em) is
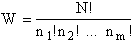 (6)
(6)
For example, if we have N=20 molecules shared in four energy levels (e1, e2, e3, e4) as
shown below

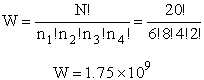
there are 1.75x109 ways to arrange the 20 molecules among the four energy
levels shown. There are better ways to put the 20 molecules in the four energy states to arrive at a number of
arrangements greater than 1.75x109. What are they?
For a constant total energy, E, there will be a
maximum in W, the number of possible arrangements and this arrangement will overwhelm the rest. Consequently, the
system will most always be found in that arrangement. Differentiating Eqn. (3) and setting dW = 0, we find
the distribution that gives this maximum [see A6p571]. The fraction of molecules in energy state ei is
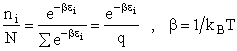 (7)
(7)
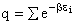 (8)
(8)
The molecular partition function q, measures how the molecules are distributed (i.e. partitioned)
over the available energy states.
Equation (7) is the Boltzmann Distribution. It
is the most probable distribution of N molecules among all energy states ei from i=0 to i=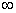 subject to
the constraints that the total number of molecules N and the total energy, E are constant.
subject to
the constraints that the total number of molecules N and the total energy, E are constant.
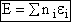 (5)
(5)
This energy E = 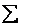 ni ei is relative to the lowest
energy, U0, (the ground state) the value at T=0. To this internal energy, E, we
must add the energy at zero degrees Kelvin, U0 (A6p579) to obtain the total
internal energy
ni ei is relative to the lowest
energy, U0, (the ground state) the value at T=0. To this internal energy, E, we
must add the energy at zero degrees Kelvin, U0 (A6p579) to obtain the total
internal energy
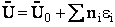 (9)
(9)
The tildes, 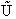 , represent that this is the total energy
not the energy per mole.
, represent that this is the total energy
not the energy per mole.
Comments on the Partition Function q
The molecular partition function gives an indication of the average number of states that are thermally
accessible to a molecule at the temperature of the system. At low temperatures only the ground state is accessible.
Consider what happens as we go to the extremes of temperature.
(a) At high temperatures, (kT ≥≥ 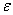 i), most all states are accessible.
i), most all states are accessible.
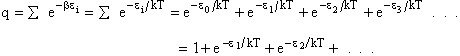
Now as 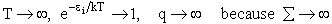
i.e.
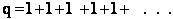
and we see the partition function goes to infinity as all energy states are accessible.
(b) At the other extreme, very very low temperatures (kT << 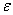 i).
i).
as
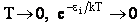
then 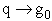
and we see that none of the states are accessible with one exception, namely degeneracy
in the ground state, i.e., 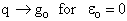
B. Relating  , ni and N
, ni and N
W is the number of ways of realizing a distribution for N particles distributed on ei levels for a total energy E
E = 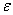 1n1 +
1n1 + 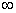 2n2 +
2n2 + 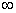 3n3 + .
. .
3n3 + .
. .
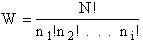 (6)
(6)
ei
The Basic Postulate is
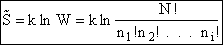 (10)
(10)
Next we relate 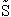 and q through W
and q through W
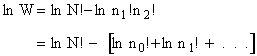
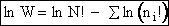 (11)
(11)
Stirling's approximation for the ln of factorials is
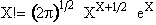
or approximately
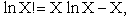 (12)
(12)
For our system this approximation becomes
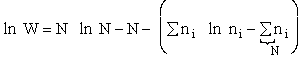 (13)
(13)
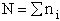 (4)
(4)
Recall substituting Eqn. (4) in Eqn. (13) we find
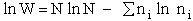
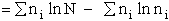
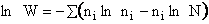
Further rearrangement gives
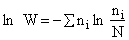 (14)
(14)
combining Eqns. (10) and (14)
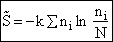 (15)
(15)
C. Relate 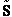 and q
and q
Recall that the fraction of molecules in the ith energy state is
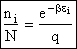 (8)
(8)
Taking the natural log of Eqn. (5)
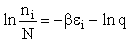
Substituting for 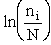 in Eqn. (13)
in Eqn. (13)
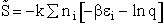
Rearranging
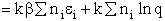
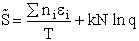
Recall from Eqn. (9) for = E = Uo, where Uo o, where Uo is the ground state
energy in kcal.
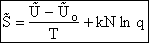 (16)
(16)
This result is for non interacting molecules. We now must extend/generalize our conclusion to include systems of
interacting molecules. The molecular partition function, q, is based on the assumption the molecules are independent
and don't interact. To account for interacting molecules distributed in different energy states we must consider
the Canonical partition function, Q.
D. Canonical Partition Function for Interacting Molecules
Canonical ensemble (collection) (A6p583)
We now will consider interacting molecules and to do this we must use the Canonical ensemble which is a collection
of systems at the same temperature T, volume V, and number of molecules N. These systems can exchange energy with
each other.

Let
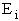 = Energy of ensemble i
= Energy of ensemble i
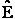 = Total energy of all the systems
= Total energy of all the systems 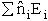 = a constant
= a constant
 = Number of members of the ensemble with energy EI
= Number of members of the ensemble with energy EI
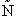 = Total number of ensembles
= Total number of ensembles
Let Pi be the probability of occurrence that a member of the ensemble has an
energy Ei. The fraction of members of the ensemble with energy Ei can be derived in a manner similar to the molecular partition function.
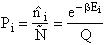
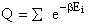 (17)
(17)
Q is the Canonical Partition Function.
We now rate the Canonical partition function
the molecular partition function (A6p858). The energy of ensemble i, Ei, is the
sum of the energies of each of the molecules in the ensembles
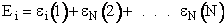
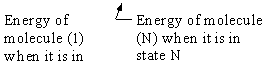

Expanding the i=1 and i=2 terms
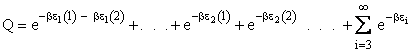
Each molecule, e.g. molecule (1), is likely to occupy all the states available to it. Consequently, instead of
summing over the states i of the system we can sum over the states i of molecule 1, molecule 2, etc.
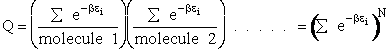
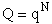
This result (Eqn. (17)) is for distinguishable molecules.
However, for indistinguishable molecules it doesn't matter which molecule is in which state, i.e.,
whether molecule (1) is in state (a) or (b) or (c)
(1)  (a) (1)
(a) (1)  (b) (1)
(b) (1)  (c)
(c)
(2)  (b) (2)
(b) (2)  (c) (2)
(c) (2)  (a)
E =
(a)
E = 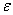 a +
a + 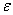 b +
b + 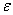 c
c
(3)  (c) (3)
(c) (3)  (a) (3)
(a) (3)  (b) (etc)
(b) (etc)
Consequently we have to divide by N!
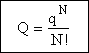 (18)
(18)
The molecular partition function is just the product of the partition functions for translational
(qT), vibrational (qV), rotational
(qR) and electronic energy (qE) partition
functions.
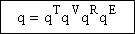 (19)
(19)
This molecular partition function, q, describes molecules that are not interacting. For interacting particles we
have to use the canonical ensemble. We can do a similar analysis on the canonical ensemble [collection] to obtain
[A5p684]
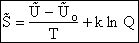 (20)
(20)
Combining Equations (17) and (20) thus
Which is a result we have been looking for.
|
|
 (22)
(22)
E. Thermodynamic relationships to relate 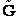 ,
,
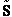 and q
and q
We now are going to use the various thermodynamic relationships to relate the molecular partition function to
change in free energy DG. Then we can finally relate the molecular partition function to the
equilibrium constant K. From thermodynamic relationships we know that the Gibbs Free Energy, 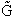 , can be written as
, can be written as
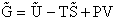 (23)
(23)
For an ideal gas with n total moles
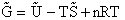 (24)
(24)
Again we note the dimensions of 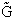 are energy (e.g.
kcal or kJ) and not energy/mol (e.g. kcal/mol). Combining Equations (20) and (24) for
are energy (e.g.
kcal or kJ) and not energy/mol (e.g. kcal/mol). Combining Equations (20) and (24) for 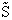 and
and 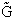 we obtain
we obtain
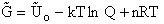 (25)
(25)
Recalling the relationship of Q to the molecular partition function
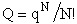 (18)
(18)
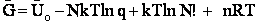 (26)
(26)
We use Avogadro's number to relate the number of molecules N and moles n, i.e., N = nNavo, along with the Stirling approximation to obtain
 (27)
(27)
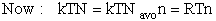
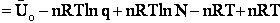
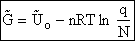 (28)
(28)
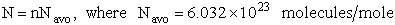
F. Relate G, the molar partition function qm
We divide by the number of moles, n to get
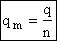 (29)
(29)
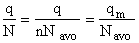
Substituting for (q/N) in Eqn. (28)
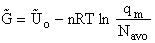 (30)
(30)
To put our thermodynamic variables on a per mole basis (i.e., the Gibbs free energy and the internal energy) we
divide by n, the number of moles.
This is a result we have been looking for
|
|
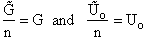
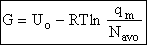 (31)
(31)
where G and Uo are on a per mole basis and are in units such as (kJ/mol) or
(kcal/mol).
G. Relating the dimensionless equilibrium constant K and the molar partition function qm
Applying Eqn. (31) to species i
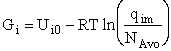
For the reaction
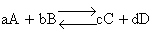
the change in Gibbs free energy is
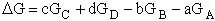 (32)
(32)
Combining Eqns. (31) and (32)
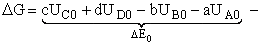
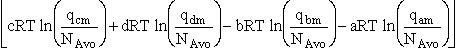
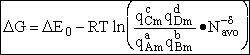 (33)
(33)
where again
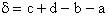
From thermodynamic and Appendix C we know
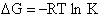
Dividing by RT and taking the antilog
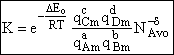 (34)
(34)
H. Relate the molecular partition function on a basis of per unit volume, q' and the equilibrium constant
K
The molecular partition function q is just the product of the electronic, qE,
translational, qT, vibrational, qV, and
rotational, qR partition functions
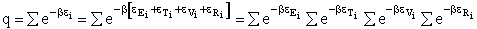
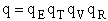 (19)
(19)
Equations for each of these partition functions 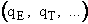 will be
given later. We now want to put the molecular partition function on a per unit volume basis. We will do this by
putting the translational partition function on a per unit volume basis. This result comes naturally when we write
the equation for qT
will be
given later. We now want to put the molecular partition function on a per unit volume basis. We will do this by
putting the translational partition function on a per unit volume basis. This result comes naturally when we write
the equation for qT
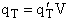 (35)
(35)
therefore
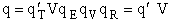 (36)
(36)
and
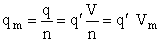 (37)
(37)
By putting 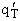 on a per unit volume basis we put the
product
on a per unit volume basis we put the
product 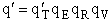 on a per unit volume basis. The prime again
denotes the fact that the transitional partition function, and hence the overall molecular partition function, is on
per unit volume.
on a per unit volume basis. The prime again
denotes the fact that the transitional partition function, and hence the overall molecular partition function, is on
per unit volume.
The molar volume is
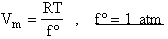
where f° is the fugacity of the standard state of a gas and is equal to 1 atm.
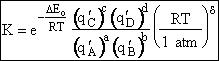 (38)
(38)
(See Appendix TS2 page 29 of Transition State Theory Notes for derivation)
I. Recall the relationship between K and KC from Appendix C.
The equilibrium constant and free energy are related by
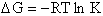
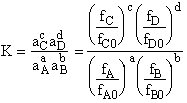 (39)
(39)
The standard state is fi0 = 1 atm. The fugacity is given by fA = gAPA [See Appendix C of text]
 (40)
(40)
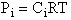
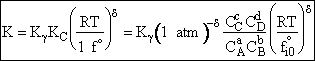 (41)
(41)
For an ideal gas 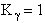
Equating Eqns. (40) and (41) and canceling 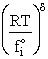 on both sides
on both sides
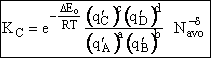 (42)
(42)
Now back to our transition state reaction
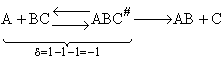
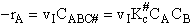 (c)
(c)
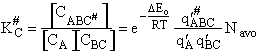 (43)
(43)
where 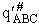 is the molecular partition function per unit
volume for the activated complex.
is the molecular partition function per unit
volume for the activated complex.
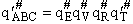 (44)
(44)
Rearranging Eqn. (43), we solve for the concentration of the activated complex 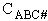
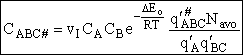 (45)
(45)
J. The Loose Vibration, vI
We consider the dissociation of ABC# as a loose vibration with
frequency vI in that the transition state molecule
ABC# dissociates when it crosses the barrier. Therefore the rate of
dissociation is just the vibrational frequency at which it dissociates times the concentration of
ABC# (Lp96)
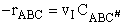 (46)
(46)
Substituting Eqn. (45) into Eqn. (46)
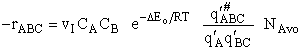
Where q¢ is the partition function per unit volume. Where vI is the "imaginary" dissociation frequency of crossing the barrier
The vibrational partition, 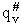 , function is the product of the partition function for all vibrations
, function is the product of the partition function for all vibrations
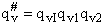 (47)
(47)
Factoring out qvI for the frequency of crossing the barrier
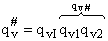
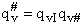 (48)
(48)
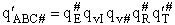 (49)
(49)
Note we have moved the # from a superscript to subscript to denote that 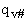 is the vibrational partition function less the imaginary mode
vI.
is the vibrational partition function less the imaginary mode
vI. 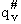 is the
vibrational partition function for all modes of vibration, including the imaginary dissociation frequency (Lp96).
is the
vibrational partition function for all modes of vibration, including the imaginary dissociation frequency (Lp96).
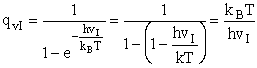 (50)
(50)
 (51)
(51)
This is the result we have been looking
for!
|
|
Substituting for 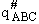 in Eqn. (45) and
canceling vI
in Eqn. (45) and
canceling vI
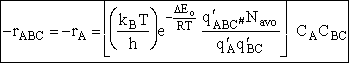 (52)
(52)
where 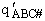 is the partition function per unit volume
with the partition function for the vibration frequency for crossing removed.
is the partition function per unit volume
with the partition function for the vibration frequency for crossing removed.
q = molecular partition function 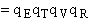
q' = molecular partition function per unit volume
q = q' V
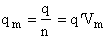 molar partition function
molar partition function
q'# = Partition function (per unit volume) of
activated complex that includes partition function of the vibration frequency vI,
the frequency of crossing
q'# = Partition function (per unit volume) of the
activated complex but does not include the partition function of the loose vibration for crossing the barrier
What are the Equations for q'T, qV, qE, and
qR
K. Evaluating the Partition Functions
Schrödinger Wave Equation
We will use the Schrödinger wave equation to obtain the molecular partition functions. The energy of the
molecule can be obtained from solutions to the Schrödinger wave equation (A5p370)
 (53)
(53)
This equation describes the wave function, y, for a particle (molecule) of mass m and
energy E traveling in a potential energy surface V(x,y,z). "h" is Planck's constant. The one
dimensional form is
 (54)
(54)
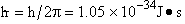
The probability of finding a particle in a region between x and x+dx is
Probability = 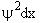
 is the probability density (A5p373)
is the probability density (A5p373)
et, eV,
and eR) used in the partition function q. The equation is
solved for three special cases
1. Translational energy,
et. Particle in a Box.
2. Vibrational energy, eV. Harmonic Oscillator.
3. Rotational Energy, eR. Rigid Rotator.
4. Electronic Energy, eE.
Recall 
The electronic partition functions qE, is most always close to one.
Table PRS.3B-2Overview of q¢
Parameter Values
1 atomic mass unit º 1 amu = 1.67x1027 kg, h = 6.626x1034kg•m2/s,
kB = 1.38x1023kg•m/s2/K/molecule
1. Transitional Partition Function 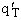
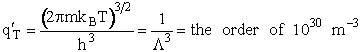 (55)
(55)
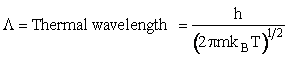


Substituting for kB, 1 amu and
Plank's constant h
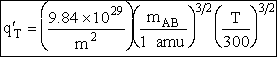 (56)
(56)
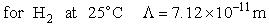
2. Vibrational Partition Function qv
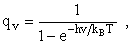 (57)
(57) 
Expanding in a Taylor series
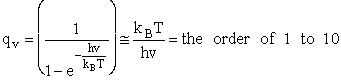
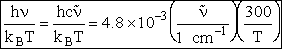 (58)
(58)
3. Electronic Partition Function
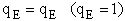

4. Rotational Partition Function qR
For linear molecules
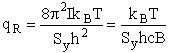 (59)
(59)
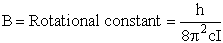
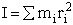

where ABC are the rotational
constants (Eqn. 57) for a nonlinear molecule about the three axes at right angles to one another
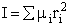
For a linear molecule
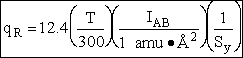 (60)
(60)
For non-linear molecules
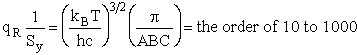
Sy = symmetry number of different but equivalent arrangements that can be made by rotating the
molecule. (See Laidler p. 99)
For the water and hydrogen
molecule Sy = 2
For HCl Sy = 1
Estimate A from Transition State Theory
Let's do an order of magnitude calculation to find the frequency factor A.
Let's first calculate the
quantity
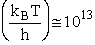
at 300K
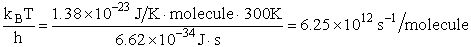
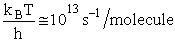
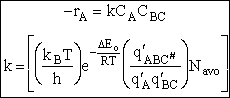 (61)
(61)
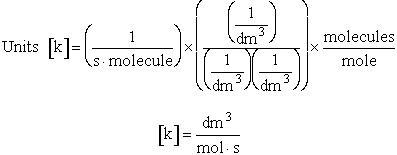
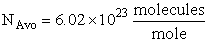
At 300K
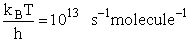
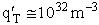
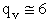

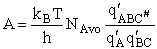
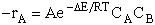
| |
A
|
BC
|
ABC
|
|
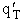
|
6 x 1032 m3
|
6 x 1032
|
6 x 1032
|
|
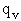
|
--
|
5
|
5
|
|
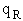
|
--
|
20
|
200
|
|
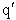
|
6 x 1032 m3
|
600 x 1032 m3
|
6000 x 1032 m3
|
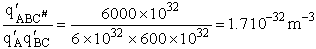
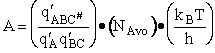
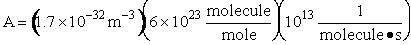
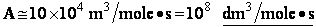
which compares with A predicted by collision theory
IV. The Eyring Equation
For the reaction
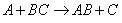
The rate law is
 (62)
(62)
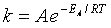 (63)
(63)
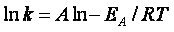 (64)
(64)
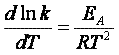 (65)
(65)
Now let's compare this withn transition state theory.
The rate of reaction is the rate at which the activated complex crosses the barrier.
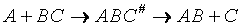
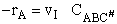 (1)
(1)
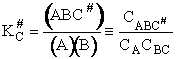 (2)
(2)
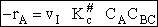 (3)
(3)
Factoring out partition function for loose vibrational frequency, vI, from the vibrational partition function, gives 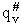
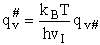 (66)
(66)
then from Eqn. (43) we can obtain
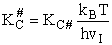 (67)
(67)
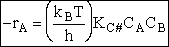 (68)
(68)
which is referred to as the Eyring Equation.
From thermodynamics
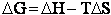 (69)
(69)
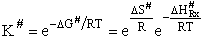 (70)
(70)
The overall dimensionless terms of mole fraction xi
and the activity coefficients gi
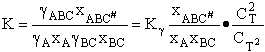 (71)
(71)
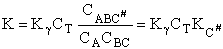 (72)
(72)
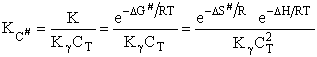 (73)
(73)
 S# will be
negative because we are going form 0 less ordered system of A, BC moving independently as reactants to a more ordered
system of A, B and C being connected in the transition state. The entropy can be thought of as the number of
configurations/orientations available for reactions. That is
S# will be
negative because we are going form 0 less ordered system of A, BC moving independently as reactants to a more ordered
system of A, B and C being connected in the transition state. The entropy can be thought of as the number of
configurations/orientations available for reactions. That is
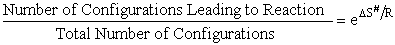
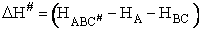
will be positive because the energy of the transition state is greater than that of the
reactant state.
Case I Liquid
For liquid
CT = a constant = CT0
(Recall for water that Cw = 55.5 mol/dm3
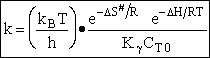 (74)
(74)
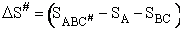 (75)
(75)
Here we see the temperature dependence as
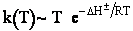
Case II Gases
Fom gases
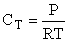
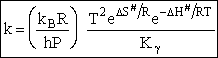
Here we see the
temperature dependence as
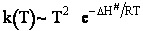
As with liquids  S# is negative and
S# is negative and 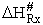 is positive.
is positive.
A and  HRx
HRx
Now lets compare the
temperature dependent terms. The heat of reaction will be positive because the activated state is at a higher energy
level than the reactants. See figure PRS.3B-2.
 (76)
(76)
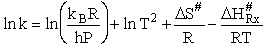 (77)
(77)
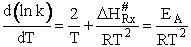 (78)
(78)
Comparing Eqns (1) and (16), the activation energy the Erying Equation is
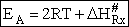 (79)
(79)
with the frequency factor
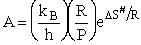 (80)
(80)
Appendix
For the general reaction

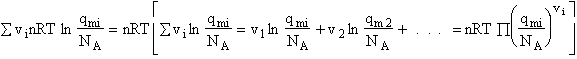
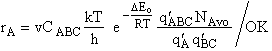
Molar partition function

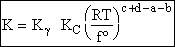
However,
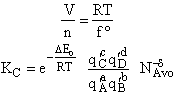
Problems
Problems for Transition State Thoery
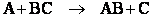
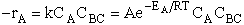
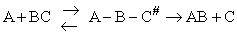
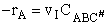
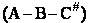 and the reactants are in
pseudo equilibrium at the top of the energy barrier.
and the reactants are in
pseudo equilibrium at the top of the energy barrier.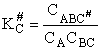
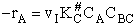
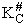 to arrive at the equation
to arrive at the equation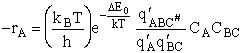
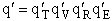
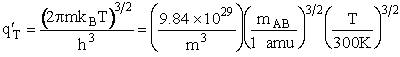
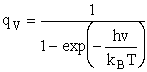
![]()
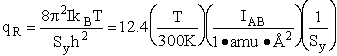
![]()
![]() for diatomic molecules
for diatomic molecules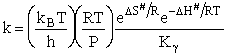




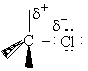
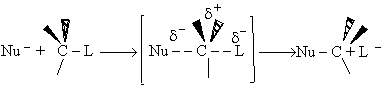

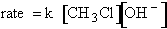


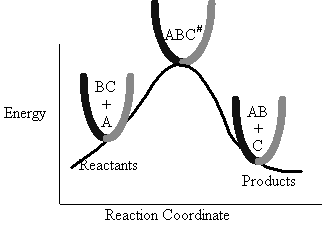

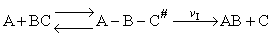
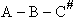 as a loose vibration of frequency v
as a loose vibration of frequency v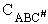
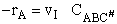 (1)
(1)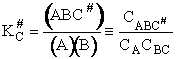 (2)
(2)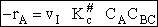 (3)
(3)

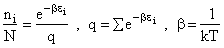
 , n
, n
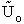 =
=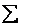 n
n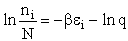
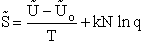
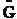 ,
, 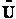 and q
and q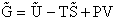
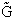 )
represents the symbols are in units of kcal or kJ without the tilde is in units per mole, e.g., kJ/mol. We first
use the last equation for S in Step 4 to substitute in the Maxwell Eqn. We next use the relationship between Q and
q, i.e.,
)
represents the symbols are in units of kcal or kJ without the tilde is in units per mole, e.g., kJ/mol. We first
use the last equation for S in Step 4 to substitute in the Maxwell Eqn. We next use the relationship between Q and
q, i.e.,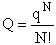
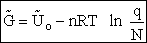
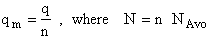
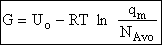
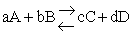
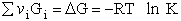

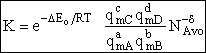
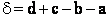
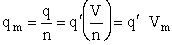
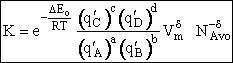
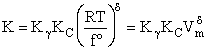
 ) to obtain K
) to obtain K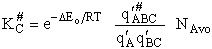
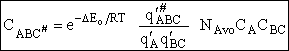

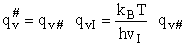
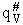 and
overall partition functions, q
and
overall partition functions, q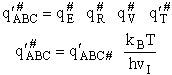
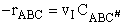 noting that v
noting that v
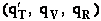
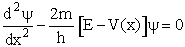
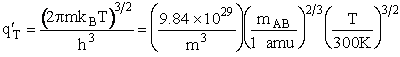
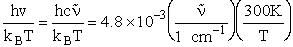
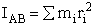

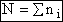 (4)
(4) = Number of molecules with energy
= Number of molecules with energy 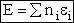 (5)
(5)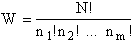 (6)
(6)
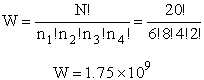
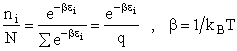 (7)
(7)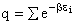 (8)
(8)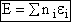 (5)
(5)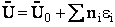 (9)
(9)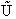 , represent that this is the total energy
not the energy per mole.
, represent that this is the total energy
not the energy per mole.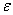 i), most all states are accessible.
i), most all states are accessible.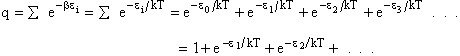
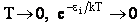
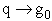
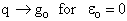
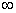
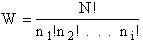 (6)
(6)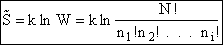 (10)
(10)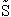 and q through W
and q through W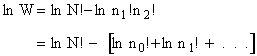
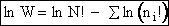 (11)
(11)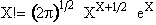
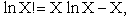 (12)
(12)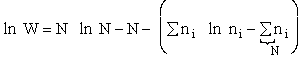 (13)
(13)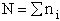 (4)
(4)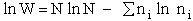
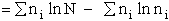
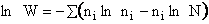
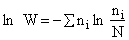 (14)
(14)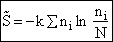 (15)
(15)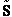 and q
and q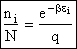 (8)
(8)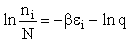
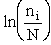 in Eqn. (13)
in Eqn. (13)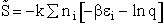
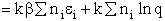
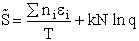
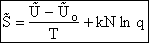 (16)
(16)
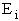 = Energy of ensemble i
= Energy of ensemble i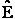 = Total energy of all the systems
= Total energy of all the systems 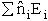 = a constant
= a constant = Number of members of the ensemble with energy EI
= Number of members of the ensemble with energy EI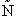 = Total number of ensembles
= Total number of ensembles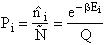
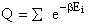 (17)
(17)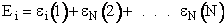
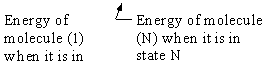

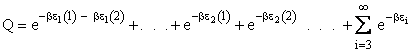
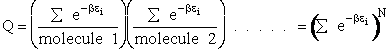
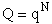
 (a) (1)
(a) (1) 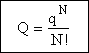 (18)
(18)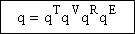 (19)
(19)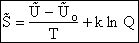 (20)
(20) (22)
(22) ,
,
 , can be written as
, can be written as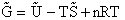 (24)
(24)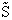 and
and 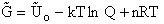 (25)
(25)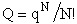 (18)
(18)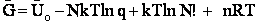 (26)
(26) (27)
(27)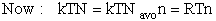
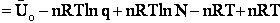
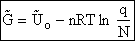 (28)
(28)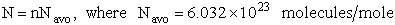
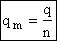 (29)
(29)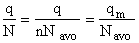
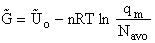 (30)
(30)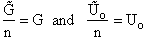
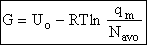 (31)
(31)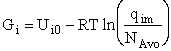
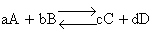
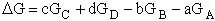 (32)
(32)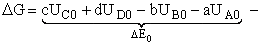
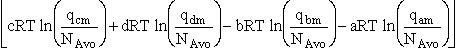
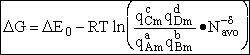 (33)
(33)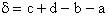
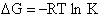
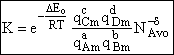 (34)
(34)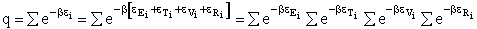
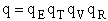 (19)
(19)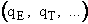 will be
given later. We now want to put the molecular partition function on a per unit volume basis. We will do this by
putting the translational partition function on a per unit volume basis. This result comes naturally when we write
the equation for q
will be
given later. We now want to put the molecular partition function on a per unit volume basis. We will do this by
putting the translational partition function on a per unit volume basis. This result comes naturally when we write
the equation for q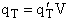 (35)
(35)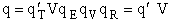 (36)
(36)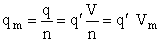 (37)
(37)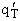 on a per unit volume basis we put the
product
on a per unit volume basis we put the
product 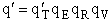 on a per unit volume basis. The prime again
denotes the fact that the transitional partition function, and hence the overall molecular partition function, is on
per unit volume.
on a per unit volume basis. The prime again
denotes the fact that the transitional partition function, and hence the overall molecular partition function, is on
per unit volume.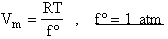
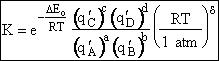 (38)
(38)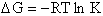
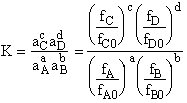 (39)
(39) (40)
(40)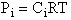
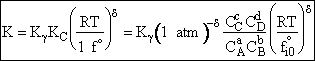 (41)
(41)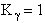
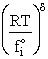 on both sides
on both sides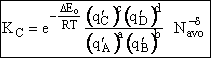 (42)
(42)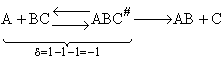
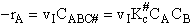 (c)
(c)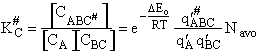 (43)
(43)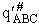 is the molecular partition function per unit
volume for the activated complex.
is the molecular partition function per unit
volume for the activated complex.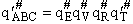 (44)
(44)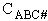
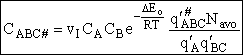 (45)
(45)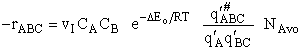
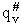 , function is the product of the partition function for all vibrations
, function is the product of the partition function for all vibrations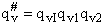 (47)
(47)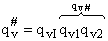
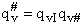 (48)
(48)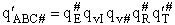 (49)
(49)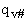 is the vibrational partition function less the imaginary mode
v
is the vibrational partition function less the imaginary mode
v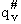 is the
vibrational partition function for all modes of vibration, including the imaginary dissociation frequency (Lp96).
is the
vibrational partition function for all modes of vibration, including the imaginary dissociation frequency (Lp96).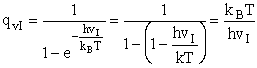 (50)
(50) (51)
(51)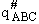 in Eqn. (45) and
canceling v
in Eqn. (45) and
canceling v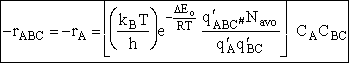 (52)
(52)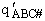 is the partition function per unit volume
with the partition function for the vibration frequency for crossing removed.
is the partition function per unit volume
with the partition function for the vibration frequency for crossing removed.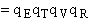
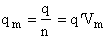 molar partition function
molar partition function (53)
(53) (54)
(54)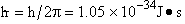
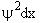
 is the probability density (A5p373)
is the probability density (A5p373)
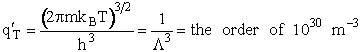 (55)
(55)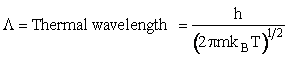


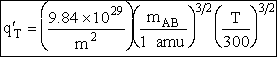 (56)
(56)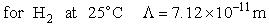
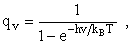 (57)
(57) 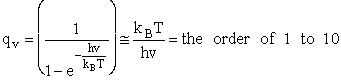
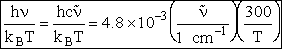 (58)
(58)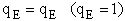
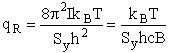 (59)
(59)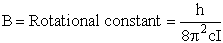
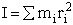
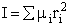
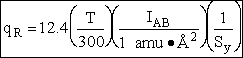 (60)
(60)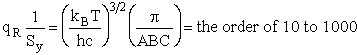

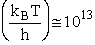
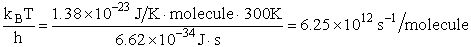
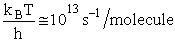
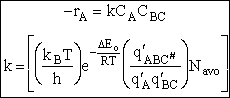 (61)
(61)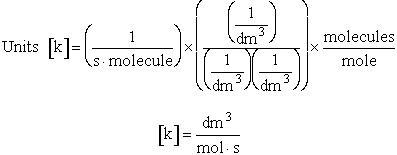
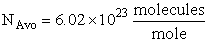
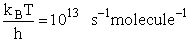
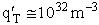
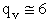

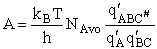
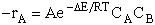
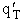
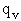
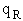
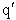
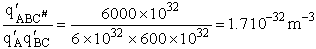
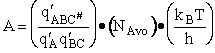
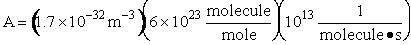
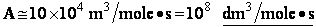
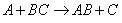
 (62)
(62)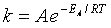 (63)
(63)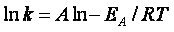 (64)
(64)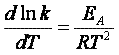 (65)
(65)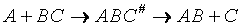
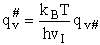 (66)
(66)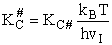 (67)
(67)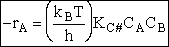 (68)
(68)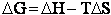 (69)
(69)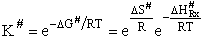 (70)
(70)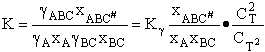 (71)
(71)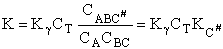 (72)
(72)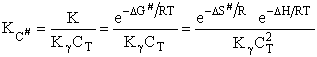 (73)
(73) S
S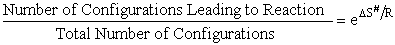
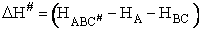
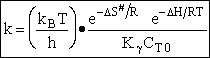 (74)
(74)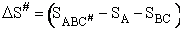 (75)
(75)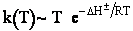
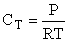
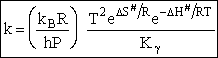
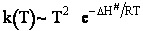
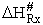 is positive.
is positive. (76)
(76)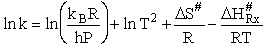 (77)
(77)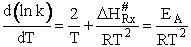 (78)
(78)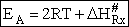 (79)
(79)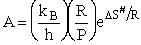 (80)
(80)