| 7 Steps in a Catalytic Reaction | top |
1. Mass transfer (diffusion) of the reactant(s) from the bulk fluid to the external
surface of the catalyst pellet
2. Diffusion of the reactant from the pore mouth through the catalyst pores to the
immediate vicinity of the internal catalytic surface
3. Adsorption of reactant A onto the catalytic surface
4. Reaction on the surface of the catalyst
5. Desorption of the products from the surface
6. Diffusion of the products from the interior of the pellet to the pore mouth at the
external surface
7. Mass transfer of the products from the external pellet surface to the bulk fluid
We shall now focus on steps 1, 2, 6, and 7. Because the reaction below does not occur in
the bulk phase (only at the surface, at z = delta), we shall first consider steps 1 and 7.
Diffusion is the spontaneous intermingling or mixing of atoms or molecules
by random thermal motion. Mass transfer is any process in which diffusion
plays a role.
The molar flux is just the molar flow rate, FA, divided by the
cross sectional area, AC, normal to the flow. WA =
FA/AC
Molar flux of A WA (moles/time/area) with respect to fixed coordinate system
WA = JA + BA
JA = diffusional flux of A with respect to bulk motion, i.e. molar average velocity
BA = flux of A resulting from bulk flow
One dimension for constant total concentration- Ficks First Law
![]()

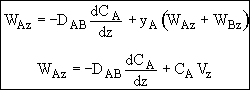
Gases: DAb~10-5m2/s
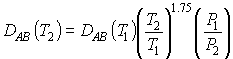
Liquids: DAb~10-9m2/s
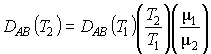
| External Diffusion Across a Stagnant Film | top |
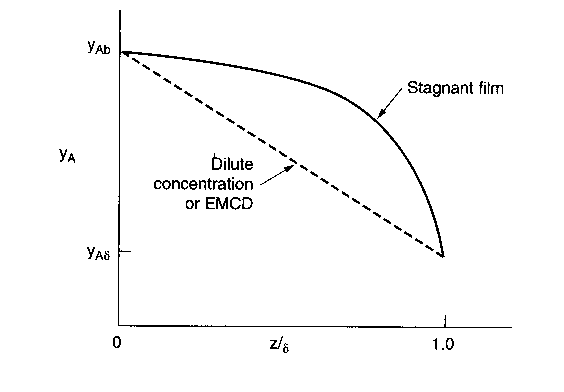
Species A diffuses from the bulk (z=0) to a catalytic surface (z=d) where it reacts instantaneously to form B.
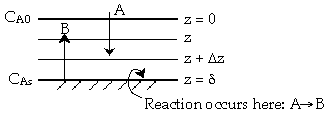
In-Out+Generation=Accumulation
![]()
![]()
![]()
Types of Boundary Conditions1. Specify a concentration a boundary
2. Specify a flux at a boundary a) No mass transfer across a boundary [E.g., at pipe wall]
therefore
b) Reaction at a boundary
c) Diffusional flux to a boundary is equal to the convective flux away from the boundary.
e.g.,
3. Planes of Symmetry [E.g., cylinder]
|
1) Dilute concentrations (liquids)
Constant total concentration
2) Equal Molar Counter Diffusion (EMCD)
3) Diffusion through a Stagnant Film
|
| Relaitve Rates of Diffusion and Reaction | top |
| 1. | Mole Balance on Species A at steady state |
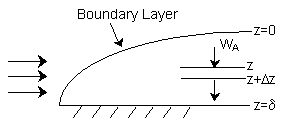
|
|
Integrating: |
|
WA=K' |
|
| 2. | Rate Law / Constitutive Equation |
Constitutive Equation |
|
|
|
Rate Law on Surface |
|
| 3. | Boundary Conditions |
Z=0 CA=CA0 |
|
Z=d CA=CA0 |
|
The rate of arrival of molecules on the surface equals the rate of reaction on the surface.
|
|
|
|
kC is the mass transfer transfer coefficient. It can be found from a correlation for the Sherwood number: |
|
which in turn is a function of the Reynolds Number |
|
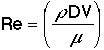 |
|
and the Schmidt Number |
|
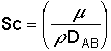 |
|
For packed beds: |
|
 |
|
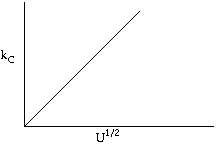
We see if we increased the velocity by a factor of 4, then the mass transfer coefficient, and hence the rate would increase by a factor of 2. |
|
The flux to the surface is equal to the rate of reaction on the surface: |
|
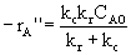 |
|
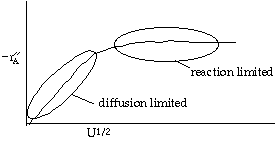
Let's look at the effect of increasing the velocity. We know that kc increases with increasing velocity, while kr is independent of velocity. At low velocities, the reaction is diffusion limited with kc >>kr and -rA=kc CAO |
|
| CASE 1 when kc >>> kr, then reaction is diffusion limited |
|
|
|
| CASE 2 when kc >>> kr, then reaction is reaction rate limited |
|
|
|
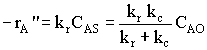 |
|
 |
|
At high velocities, kc >> kr and -rA is independent of velocity |
|
 |
| Mass Transfer in a Packed Bed of Catalyst Particles | top |
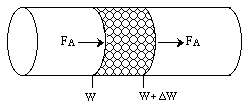
Mole Balance |
||
Rate Law / Constitutive Equation |
||
|
||
|
||
If |
||
kr >>> kc |
||
Then |
||
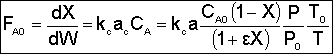 |
||
We want to know how the mass transfer coefficient varies with the physical properties (e.g., DAB) and the system operating variables. |
||
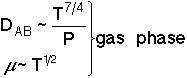 |
||
For isothermal operation, taking the rates for case 1 and case 2, the product of the mass transfer coefficient and the area acis |
||
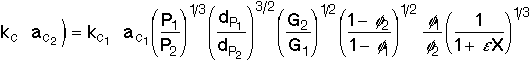
|
||
This equation tells us how the product of our mass transfer coefficient and surface area would change, if we were to change our operating conditions. In other words, it will help us answer "What if..." questions about our system. |
||
For example: What effect does pressure drop have when all other variables remain the same? |
||
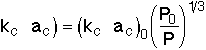 |
||
For |
||
Substituting: |
||
If |
||
Then |
||
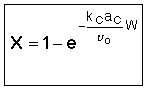 |
||
| Shrinking Core Model | top |

![]()
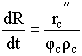
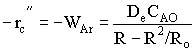
Time to complete consumption, tc
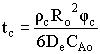
* All chapter references are for the 4th Edition of the text Elements of Chemical Reaction Engineering .