14. Models for Nonideal Reactors*


Topics

  1. One Parameter Models
  2. Two Parameter Models

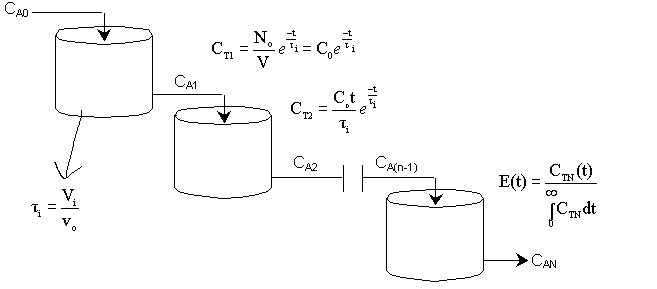
One Parameter Models top

A.  Tanks-In-Series    

A real reactor will be modeled as a number of equally sized tanks-in-series. Each tank behaves as an ideal CSTR.  The number of tanks necessary, n (our one parameter), is determined from the E(t) curve.

For n tanks in series, E(t) is

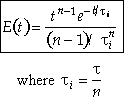
It can be shown that

In dimensionless form

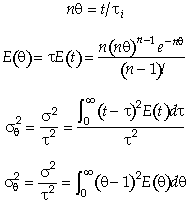
Carrying out the integration for the n tanks-in-series E(t)

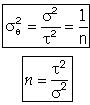
For a first order reaction

For reactions other than first order and for multiple reactions the sequential equations must be solved


 

B.  Dispersion Model

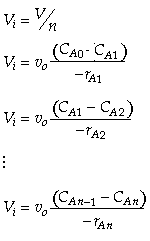
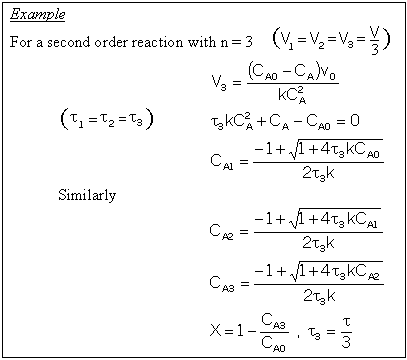
The one parameter to be determined in the dispersion model is the dispersion coefficient, Da. The dispersion model is used most often for non-ideal tubular reactors.  The dispersion coefficient can be found by a pulse tracer experiment.

 

 

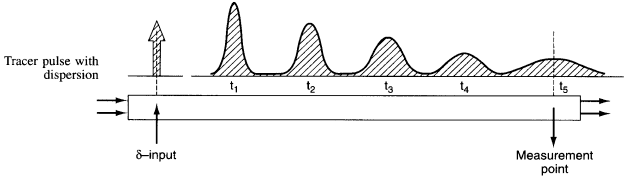
After a very, very narrow pulse of tracer is injected, molecular diffusion (and eddy diffusion in turbulent flow) cause to pulse to widen as the tracer molecules diffuse randomly in all directions.  The convective transport equation is:

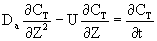
Finding the Dispersion Coefficient

1)     For laminar flow Taylor-Aris Dispersion, the molecules diffuse across radial 

        streamlines as well as axially to disperse the fluid.

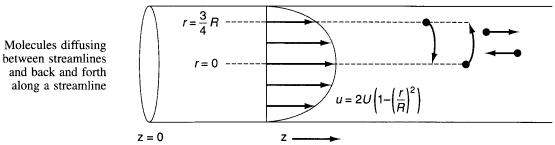
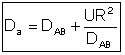
2)     To find Da for pipes in turbulent flow see Figure 14-6

3)     To find Da for packed bed reactors see Figure 14-7

    

Using the RTD to find the Dispersion Coefficient.

       Results of the tracer test can be used to determine Per from E(t).  We need to

       consider two sets of boundary conditions.

1. Closed-Closed Vessels

       2. Open-Open Vessels

            

 

For a Closed-Closed Vessel

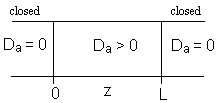
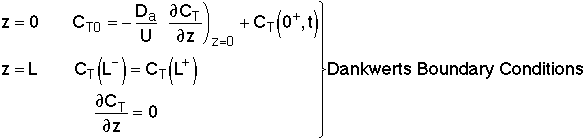
We note there is a discontinuity at the entering boundary in the tracer concentration.

 

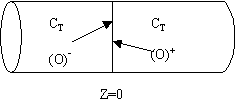
Due to the discontinuity at boundary due to forward diffusion,  Ct(O-)=Ct0>Ct(O+)

However, at the end of the reactor,  Ct(L-)=Ct(L+)

 

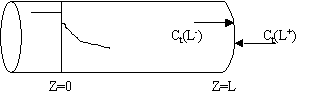
Returning to the unsteady tracer balance

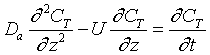(1)

Let λ = z/L, 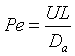and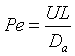

Then in dimensionless form

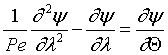
For the closed-closed boundary condition the solution to the tracer balance at the exit (λ = 1) , at any time Θ, i.e., Ψ(1,Θ) gives

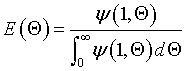
where
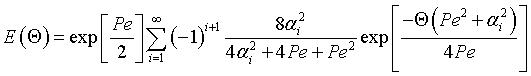(2)

From page 530 of Froment and Bischoff Chemical Reactor Analysis, 2 nd Edition, John Wiley & Sons, 1966.
     Eigen Values αi are found from the equation


For Pe = 10
           α1=1.5
           α2=2.4
           α3=4.8
           α4=5.1
           α5=7.9
           α6=8.1

F

0 ≤ λ ≤ 1

Integrating Equation (3) using Equation (2) gives
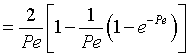(3)

We see from the equation for E(theta) that the exponential term dies out as the values of alpha i become large.

then tm and Per is found from the relationship:                                                            

 

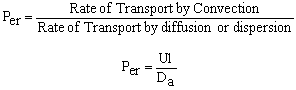
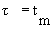
Use RTD data to calculate tm, 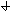2, and then Per (i.e. Da) and then use Da in calculating conversion.

For the solution to 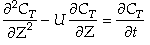with the above boundary conditions we find

    

For an Open-Open Vessel

Dispersion occurs upstream, downstream and within the reactor.

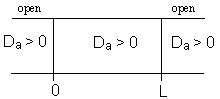
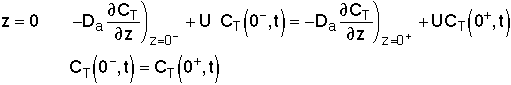
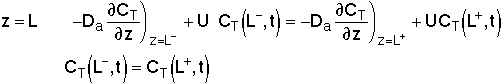
Per>100, for long tubes, the solution at the exit is 

 

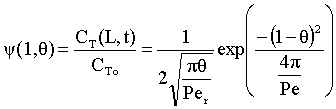
Because of the dispersion the mean residence time is greater than the space time.  The molecules can flow out of the reactor and then diffuse back in.

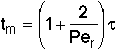
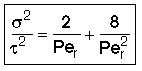
Use RTD data to calculate tm, 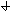2, and then Per (i.e. Da) and then use Da in calculating conversion. It can be shown that at steady state, the open-open boundary conditions reduce to the Dankwerts Boundary Conditions.

 
Sketch of F curves

 

Dispersion with Reaction

For a First Order Reaction

        

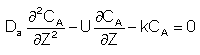
Let Ψ = CA/CA0, λ = z/L , Pe = UL/Da , and Da = kτ. The dimensionless balance on the concentration of A in the reaction zone is

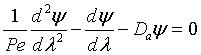
Danckwerts Boundary conditions

At λ = 0 then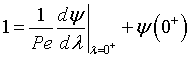

At λ = 1, then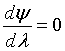

the solution is [See John B. Butt, Reaction Kinetics and Reactor Design, 2 nd Edition, page 378, Marcel Dekker, 2000.]

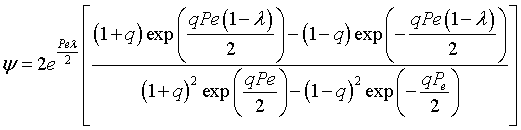
where

The Polymath program used to plot Ψ versus λ is given below

Polymath Program

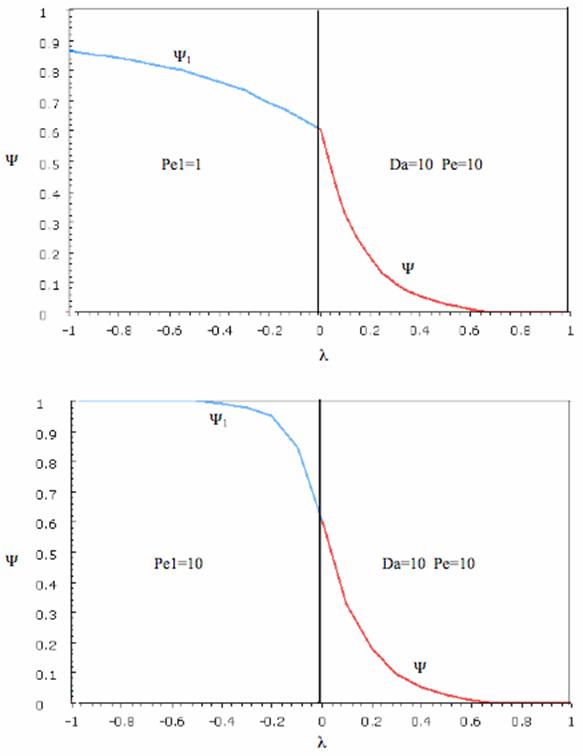
Sketches of the dimensionless concentration profiles for different values of Peclet and Damköhler numbers are shown below

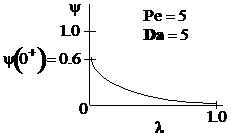
Note how Ψ(0+) changes as Pe and Da change.

     The exit conversion is

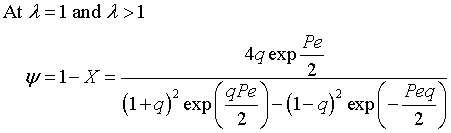
The following figures given the Polymath solutions for y versus l for different values of Pe and Da

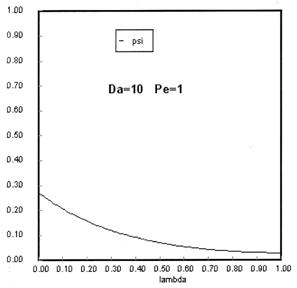
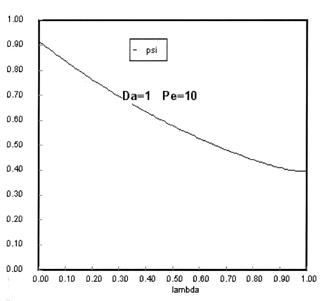
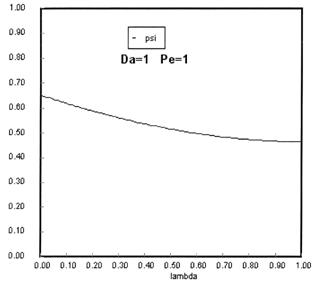
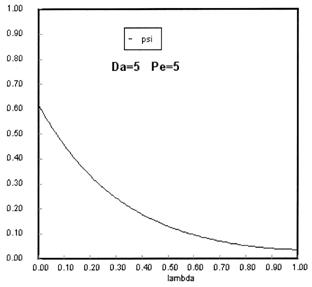
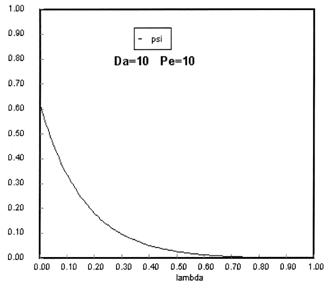
Open Open System

Upstream of the reaction zone the balance on A in dimensionless form is

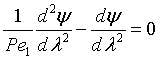
For these boundary conditions

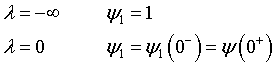
the solution is

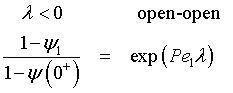
Rearranging

A typical profile is

 

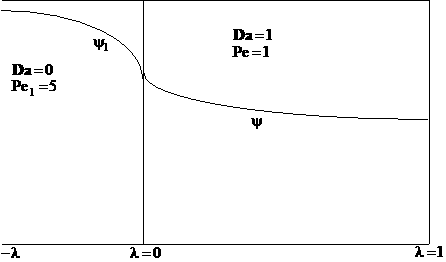
The following profiles were obtained from the Polymath Program given above. Here Ψ1 is the dimensionless concentration of A upstream of the reaction section where Da is greater than zero and Ψ is the dimensionless concentration of A in the reaction section.

Use RTD data to calculate tm, 2, and then Per (i.e. Da) and then use Da in calculating conversion.
 
   

Two Parameter Models top

The goal is to model the real reactor with combinations of ideal reactors.

CSTR with Bypass and Dead Volume

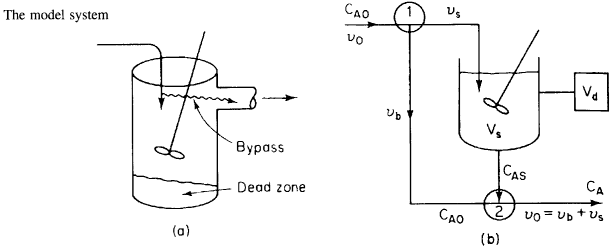
Two parameters and , the fraction of volume that is well-mixed (alpha), and the fraction of the stream that is bypassed (beta).

   

Reactor Balance


We now find the parameters a and b from a tracer experiment. We will choose a step tracer input

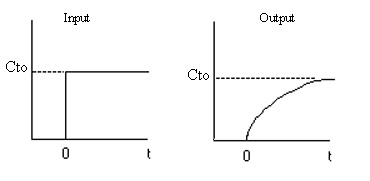
The balance equations are:

 
Finding a two parameter model

OTHER SCHEME INCLUDED

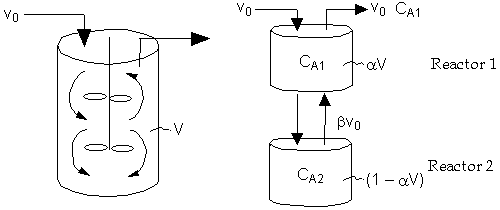
          Real Reactor                      Model  of Reactor

Two parameters, and :



  1. Use the tracer data to find and .

  2. Then use the mole balances and the rate law to solve for CA1 and CA2.

    Reactor 1:
    (Eqn. A)
    Rate Law:
    for a first order reaction or

    for a second order reaction

    Reactor 2:
    (Eqn. B)
    Rate Law:
    Solve Equations (A) and (B) to obtain CA1 as a function of , , k, , and CA0.

Overall Conversion

 
Other Scheme For Evaluation
Object Assessment of Chapter 14

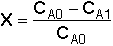
  * All chapter references are for the 4th Edition of the text Elements of Chemical Reaction Engineering .

top