| Residence Time Distribution | top |
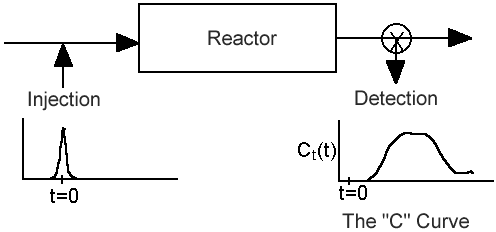
We shall use the RTD to characterize existing (i.e. real) reactors and then use it to predict exit conversions and concentrations when reactions occur in these reactors.
Inject a tracer and measure exit concentration, CT(t).

From the exit tracer concentration we can determine the following information:
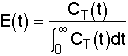
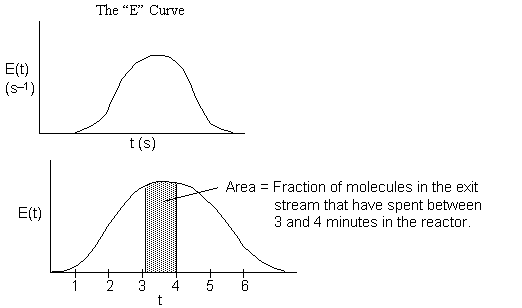
 = Fraction of molecules exiting the reactor that have spent a time between (t) and
(t + dt) in the reactor.
= Fraction of molecules exiting the reactor that have spent a time between (t) and
(t + dt) in the reactor.
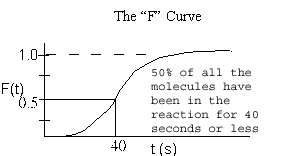
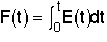 = Fraction of molecules exiting the reactor that have spent a time t or less in the reactor.
= Fraction of molecules exiting the reactor that have spent a time t or less in the reactor.
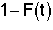 = Fraction of molecules that have spent a time t or greater in the reactor.
= Fraction of molecules that have spent a time t or greater in the reactor.
1. Mean Residence Time
2. Variance
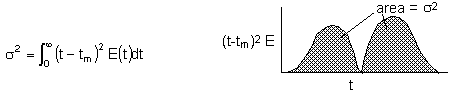
3. Space Time - For no dispersion/diffusion and v = v0, the space time equals the mean residence time.
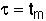
4. Internal Age Distribution,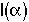
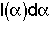 = Fraction of molecules inside the reactor that have been inside the reactor between a time
= Fraction of molecules inside the reactor that have been inside the reactor between a time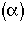 and
and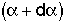 .
.
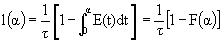
5. Life Expectancy
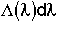 = Fraction of molecules inside the reactor with age
= Fraction of molecules inside the reactor with age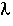 that are expected to leave the reactor in a time
that are expected to leave the reactor in a time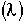 to
to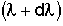 .
.
From our experimental data of the exit tracer concentration from pulse trace test
|
t(min) |
: |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
|
C(mg/m3) |
: |
0 |
0 |
0.1 |
0.2 |
0.3 |
0.1 |
0 |
We can obtain

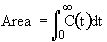 ->
->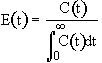 ->
-> 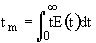 ->
-> 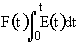 ->
->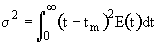
| RTD for Ideal Reactors | top |
 for Ideal Reactors for Ideal Reactors
|
||
| PFR- Inject a pulse at t=0 | 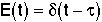
|
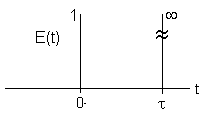
|
Dirac Delta Function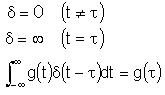
|
||
| CSTR | 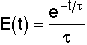
|
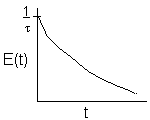
|
|
| Laminar (LFR) | 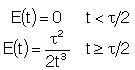
|
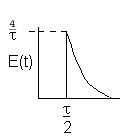
|
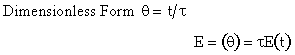
|
| RTD to Diagnose Faulty Operation | top |
Experimentally injecting and measureing the tracer in a laminar flow reactor can be a difficult task, if not a nightmare. For example, if one uses tracer chemicals that are photo-activated as they enter the reactor, the analysis and interpretation of E(t) from the data becomes much more involved.
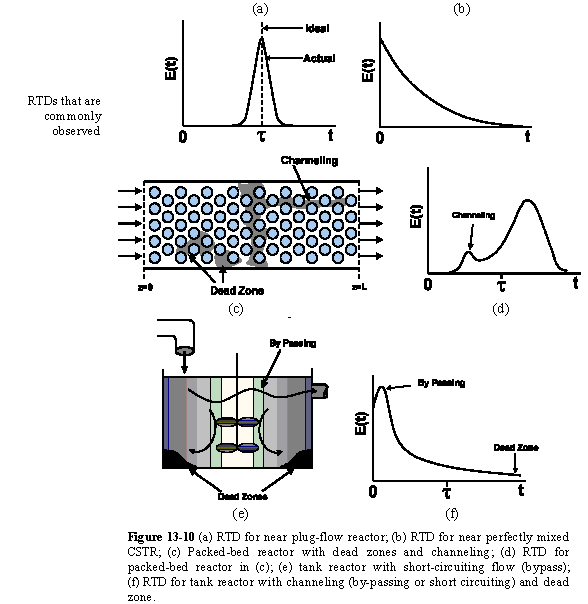
The CSTR
| Concentration | 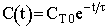 |
||
| RTD Function | 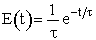 |
||
| Cumulative Function |  |
||
| Space Time | 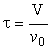 |
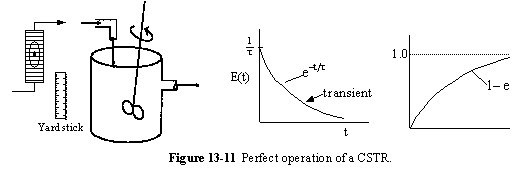
a. Perfect Operation
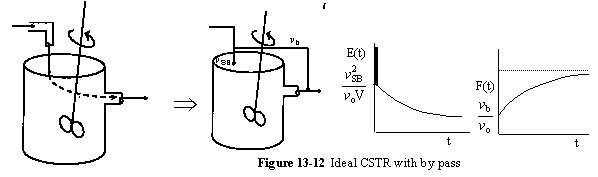
b. Passing (BP)
c. Dead Volume
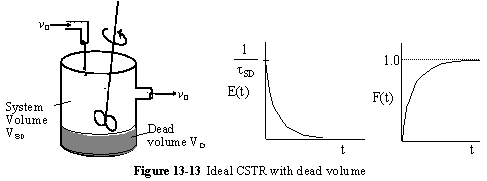
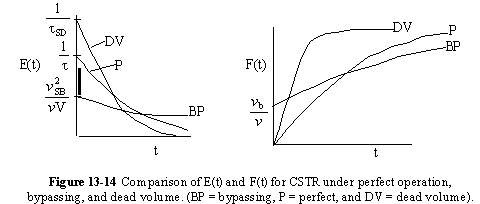
A summary for ideal CSTR mixing volume is shown in Figure 13-14
Tubular Reactor
A similar analysis to that for a CSTR can be carried out on a tubular reactor.
a. Perfect Operation of PFR (P)
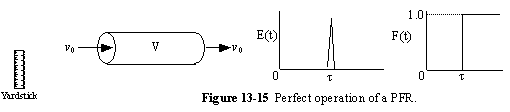
b. PFR with Channeling (Bypassing, BP)
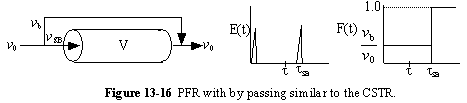
c. PFR with Dead Volume (DV)
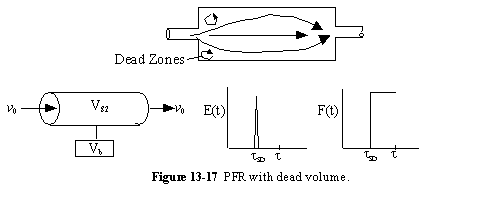
A summary for PRF is shown in Figure 13-18
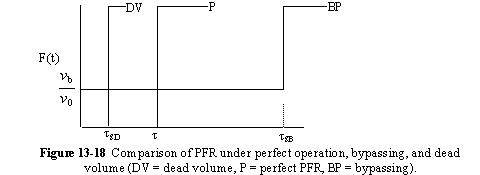
In addition to its use in diagnosis, the RTD can be used to predict conversion in existing reactors when a new reaction is tried in an old reactor. However, the RTD is not unique for a given system, and we need to develop models for the RTD to predict conversion.
| Models to Calculate the Exit Concentrations and Conversions | top |
If using mathematical software to apply the models described below, you may need to fit C(t) and E(t) to a polynomial. The procedure for fitting C(t) and E(t) to a polynomial is identical to the techniques use to fitting concentration as a function of time described in Chapter 5.
![]() Polymath regression analysis tutorial
Polymath regression analysis tutorial
Use combinations of ideal reactors to model real reactors that could also include: Zero parameter models
One parameter models
Two parameter models
|
Models the real reactor as a number of small batch reactors, each spending a different time in the reactor. All molecules that spend the same length of time in the reactor (i.e., that are of the same age) remain together in the same globule (i.e., batch reactor). Mixing of the different age groups occurs at the last possible moment at the reactor exit.
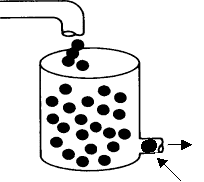 Mixing of the
globules of different ages occurs here.
Mixing of the
globules of different ages occurs here.
Little batch reactors (globules) inside a CSTR.
X3>X2>X1
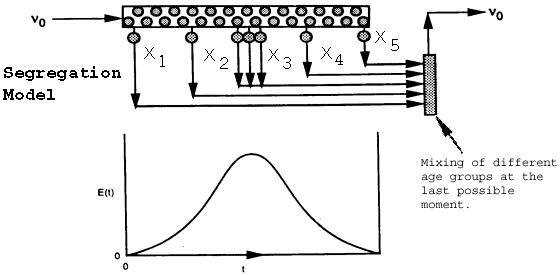
Mixing occurs at the latest possible moment.Each little batch reactor (globule) exiting the real reactor at different
times will have a different conversion. (X1,X2,X3...)
But, the mean conversion for the segregation model is
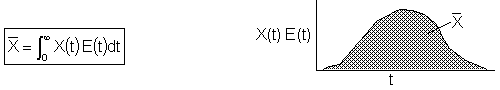
Lets apply the segregation model to an ideal PFR and see if we get the same result for conversion as we did in Chapter 4.
Solve for X(t) for a first order reaction in a batch reactor.
For the batch reactor the conversion-time relationship is
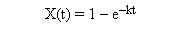
Calculate the mean conversion

which is the same conversion one finds from a mole balance (Chapter 4)
4A.2 Segregation Model Applied to an LFR
For a Laminar flow reactor the RTD function is
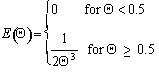
The mean conversion is
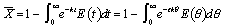
The last integral is the exponential integral and can be evaluated from tabulated values. Fortunately, Hilder developed an approximate formula
(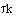 =Da).
=Da).
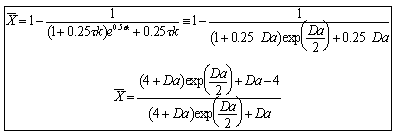
Hilder, M.H. Trans. IchemE 59 p143(1979)

For large values of the Damkohler number then there is complete conversion along the streamlines off the center streamline so that the conversion is determined along the pipe axis.
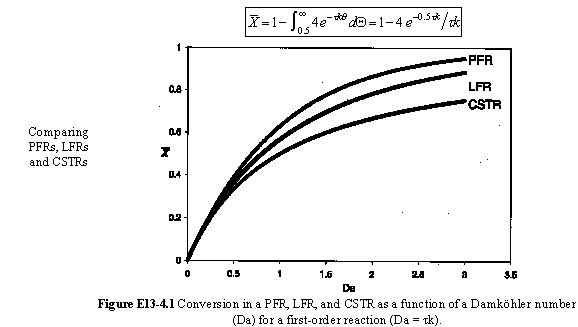
4A.3 Segregation Model Applied to a CSTR
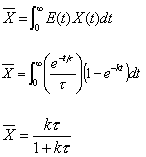
4A.4 Mean Concentration for Multiple Reactions
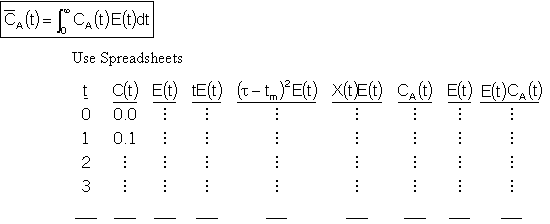
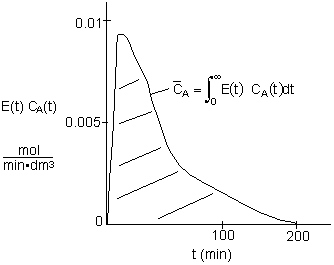
Solutions Using Software Packages
For multiple reactions use an ODE solver to couple the mole balance equations, dCi/dt=ri,
with the segregation model equations: d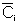 /dt=Ci(t)*E(t), where C
i is the concentration of i in the batch reactor at time t and
/dt=Ci(t)*E(t), where C
i is the concentration of i in the batch reactor at time t and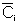 is the concentration of i after mixing the batch reactors at the exit.
is the concentration of i after mixing the batch reactors at the exit.
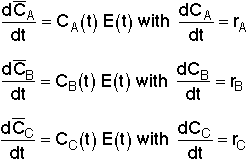
Mixing occurs at the earliest possible moment.
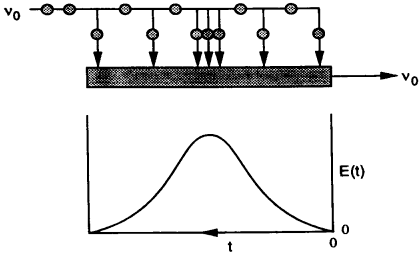
Note E(l)=E(t)
E(l)dl =Fraction of molecules that have a life expectancy between l+dl and l.
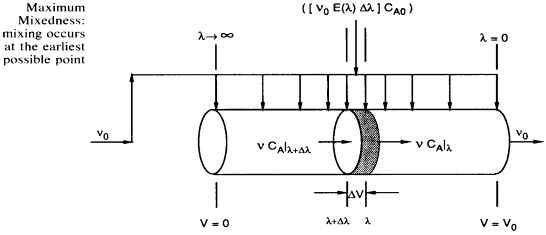
Modeling maximum mixedness as a plug flow reactor with side entrances.
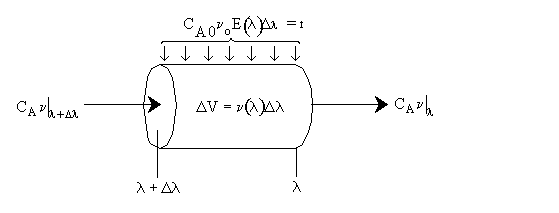
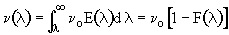
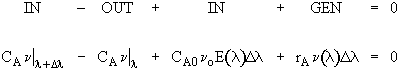
Dividing byDland taking the limit asDlgoes to zero. Substitute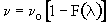 ,
,
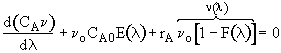 Differentiating
the first term and recalling
Differentiating
the first term and recalling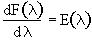 we obtain.
we obtain.
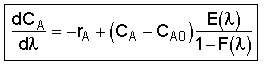
We need to integrate backwards from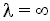 (the entrance) to
(the entrance) to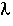 = 0
(the exit). In real systems we have some maximum value of
= 0
(the exit). In real systems we have some maximum value of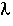 (say
(say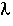 = 200 minutes) rather than
= 200 minutes) rather than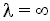 minutes. Consequently we integrate backward from
minutes. Consequently we integrate backward from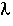 = 200. However, because most ODE packages will not integrate backwards, we have to use the transfer
= 200. However, because most ODE packages will not integrate backwards, we have to use the transfer
z = T -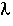 to integrate forward
to integrate forward
Thus
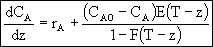
In terms of conversion,
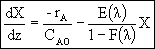
| Comparing Segregation and Maximum Mixedness Predictions | top |
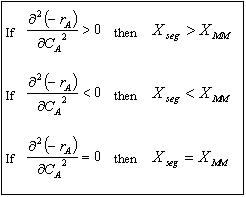
For example, if the rate law is a power law model
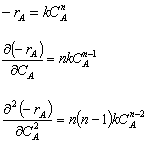
From the product [(n)(n-1)], we see
|
If n > 1, then If n < 0, then If 0 > n < 1, then |
| Multiple Reactions and RTD Data | top |
For multiple reactions use an ODE solver to couple the mole balance equations, dCi/dt=ri (where ri is the net rate of reaction), with the segregation model equations: dCi/dt=Ci(t)*E(t) as previously shown. For maximum mixedness:
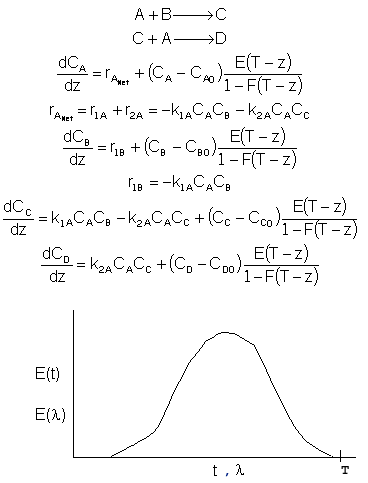
To obtain solutions with an ODE solver, first fit E(t) to a polynomial
or several polynomials. Then let
z = T -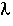 where T is the largest time in which E(t) is recorded. Proceed to solve
the resulting equations.
where T is the largest time in which E(t) is recorded. Proceed to solve
the resulting equations.
* All chapter references are for the 4th Edition of the text Elements of Chemical Reaction Engineering .