![]()
|
|
Type 8 Home Problem -- Solution
Problems that challenge assumptions.
Our first step is to select an equation to characterize the pressure drop in our system. We have chosen the following extension of the Bernoulli Equation (energy balance):
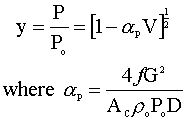
Variable definitions:


Next, we list our simultaneous differential equations:
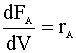
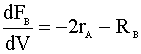

and our rate law:

Our concentrations can be written as:

The volumetric flow rate (v) will vary with the pressure and molar flow rate:
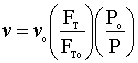
Now, we need to solve for our constants:
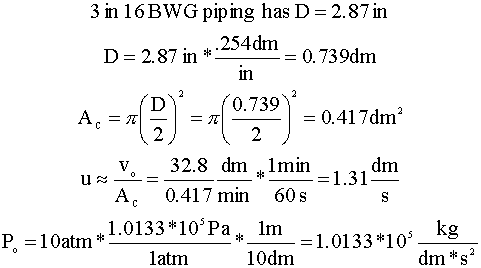
For laminar flow (Re < 2300), the friction factor (f) is inversely proportional to the Reynolds Number (Re):

For the sake of this approximation, we will assume that the density (r) is the average of the component densities (r = 0.00125 kg/dm3):
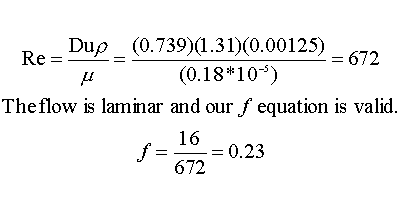
Finally, we enter these equations into Polymath:

The new conversion is almost identical to the conversion from our Homogeneous Example 7 Solution. The results are given below:
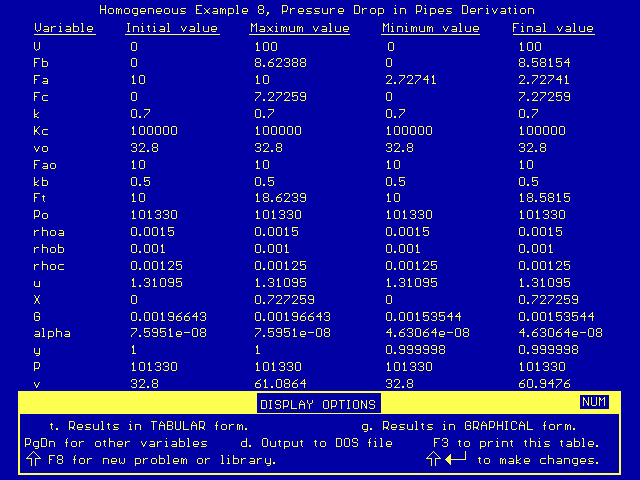
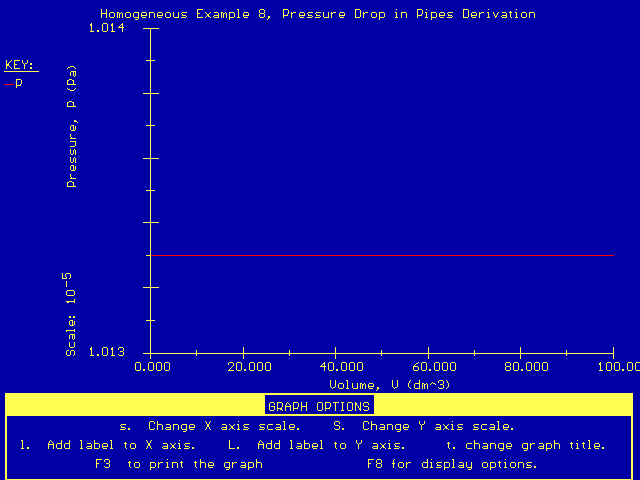
As you can see, the pressure (denoted by the variable P) did not vary substantially. This supports our previous assumption that the pressure drop for gases flowing through pipes (without packing) can be neglected.
![]() Back to Homogeneous Example 8
Back to Homogeneous Example 8
CRE Thoughts Ten Types Homogeneous Example 8