- Equations of Motion
- Estimates of the Potential Energy Surface
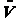 (R)
(R) - Method of Solution to Map Out Trajectories
 (1) Calculate Potential Energy Surface, (2) Carry of Trajectory Calculations The equations of motion used to calculate the trajectories in order to obtain the internuclear distances RAB, RAC, RBCare   where P is the momentum and
Non Reactive Trajectory
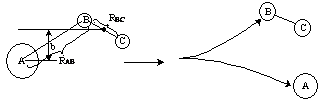  Reactive Trajectory 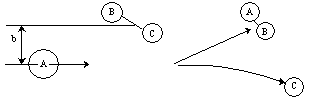  (3) We now count all the trials, N, that we carried out and all the trajectories that resulted in reaction, Nr. The probability of reaction  (4)Vary impact parameter b to obtain bmax 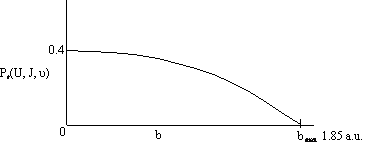 This curve can be approximated by 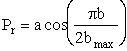 (5) Calculate Reaction Cross Section as a function of kinetic energy, velocity. 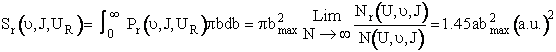 (6) Find Sr as a function of UR for a given ν and J 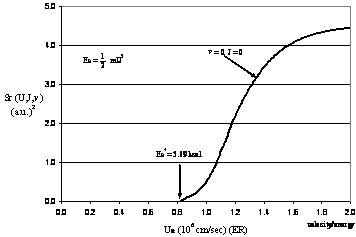 (7) Calculate reaction rate and k in vibration state ν and rotation state J 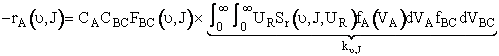 in order to obtain the overall reaction we sum over all vibrational and rotational states. To obtain the overall rate of reaction The frequency factor, A, and the activation energy, EA, calculated from molecular dynamics are in excellent with the experimental values. |
The objective of this Reference Shelf is to use molecule dynamics to provide insight as to how reactions occur. Here we will calculate reaction probabilities, reaction cross sections, and reaction rates. We will observe the effects of vibration, rotation and kinetic energies (velocity) on the colliding molecules. We will find that there is a minimum kinetic energy necessary to react, that the reaction cross section increases with increasing kinetic energy, and that there is a maximum value of the impact parameter, related to the offset of the molecular trajectories, above which no reaction will occur.
We are going to study the molecular dynamics of the reaction of the hydrogen exchange reaction
written symbolically
where molecule i has a velocity Vi and is in rotational state J and vibrational state ν. [E.g. BC (VBC, J, ν)].
We are going to consider the hydrogen exchange reaction discussed in Karplus article. †
We begin with the A and BC molecules far apart and then calculate the trajectory of the A molecule as it approaches the BC molecule. The A molecule will either replace the C molecule to form AB or it will be deflected and not react.

Let R be the distances of separation for the appropriate species. The distances of separation are shown as a function of time in Figure PRS.3C-1.
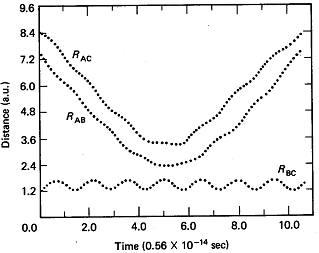
From Karplus, et.al, J.Chem. Phys. 43, p3259 (1965)
The A molecule replaces the C molecule and the RBC distance begins to increase and that the RAB distance undergoes oscillation and we see that a reaction has taken place. The time it takes the reaction to occur at t1 is about 10-14s.
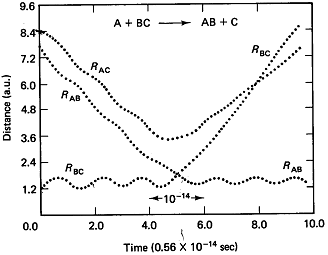
Figure
PRS.3C-2 Trajectories when a reaction occurs.
From Karplus, et.al, J. Chem. Phys. 43, p3259 (1965)
We calculate the momentum P of the molecule at a given time
and position and then calculate a new position of the molecule using only the
definition of force, F, and the potential energy surface ![]() (x).
(x).
| (C-1) | |
| (C-2) | |
| (C-3) | |
| (C-4) | |
| and | |
| (C-5) |
Equations (C-4) and (C-5) can be solved simultaneously to obtain x a function of time. Also recall the translational kinetic energy is
| (C-6) |
To solve this set of equations, [i.e., (C-4) and (C-5)]
we need the potential energy as a function of distance,
i.e., ![]() . Similarly,
for the reaction (A + BC
. Similarly,
for the reaction (A + BC ![]() AB + C)
we need the potential energy surface
AB + C)
we need the potential energy surface ![]()
Three methods are commonly used to estimate the potential energy surface.
1) Lennard-Jones 6-12 potential
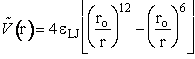
(C-7)
2) Morse potential
![]()
where εLJ is the Lennard-Jones parameter, D is
the dissociation energy, ro equilibrium internuclear distance, ![]() is the Morse potential constant.
is the Morse potential constant.
For a 3-body system ABC.†

(C-8)
where Dij is the dissociation energy for molecules i and j.
3) The Potential Energy Surface can also be calculated
a) Ab Initio [Cerius2] methods
b) Semi-empirical methods such as the London-Eyring-Polanyi-Sato
A schematic of the potential energy surface is shown in Figure PRS.3C-3.
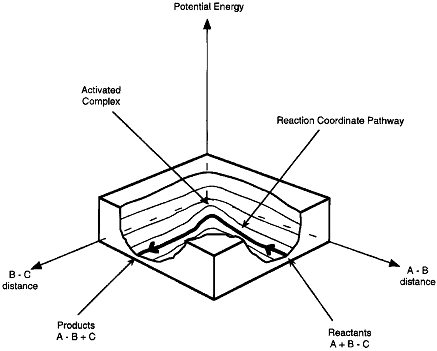
Figure PRS.3C-3 Potential energy surface.
C.1 Momentum as a function of time and position.
Consider the motion of molecule A. The x component of momentum for species A is related to the potential energy by
|
(C-9) |
| Integrating we can find the x component of momentum as a function of time and position | |
|
(C-10) |
| Similar expressions exist for y and z, e.g. | |
|
(C-11) |
| To illustrate the concept we use the Euler method of integration | |
|
(C-12) |
C.2 Location of Molecules (e.g. A) as a function of time. The position of A, i.e., x, is related to the momentum Px by the equation |
|
|
|
| Integrating we find the location of A as a function of time | |
|
(C-14) |
Because V(x) depends upon x, in practice we need to use a more sophisticated method that the Euler method (C-14) to solve these equations for Px and x simultaneously to obtain the trajectory of molecule A as a function
Table PRS.3C-1 3-D Solution Technique to Calculate Trajectory
|
|
|
|
Of course the time interval for each interaction must be small as we carry out each integration.
C.3 Calculating the Trajectories of all the Molecules Using the Hamiltonian
Because the Hamiltonian is used in classical mechanics to describe the motion of particles, let's see how it gives the same equation as those given in Table PRS.3C-1. The Hamiltonian is the sum of the kinetic and potential energies
|
(C-15) |
Differentiating the Hamiltonian w.r.t. momentum, Px, we find |
|
|
(C-16) |
|
|
Similarly |
|
|
|
We see that by using the Hamiltonian and coupling these same six equations we can trace out a trajectory for molecule A shown in Table PRS.3C-1. Change in Coordinate System A+BC→ AB + C |
|
We are going to re-design our coordinate system because we are only interested in the relative positions of the molecules to one another, not where they are in a 3-D space. This re-design is called mass weighted affine transformation. |
| Let | ||
Q1, Q2, Q3 = Location of C with B as the origin |
||
Q4, Q5, Q6 = Location of A wrt center of mass of BC |
||
Q7, Q8, Q9 = Location of Center of mass of the 3 particle system |
||
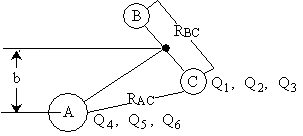 |
||
Figure PRS.3C-4 New Coordinate System. |
For example, Q1, Q2, and Q3 could represent x1, y1, and z1 components of C with B as the origin or the radial components r, Φ, and θ with r=0 as the origin. Similarly Q4, Q5, and Q6 could represent the x, y, z coordinates of A with the center mass of BC as the origin or the radial coordinates r, Φ, and θ. Knowing the location of C and A with regard to their respective origins, the distances between A and B, RAB, B and C, RBC and between A and C, RACcan easily be found. (See Figure PRS.3C-6).
In classical and statistical mechanics the Hamiltonian is used to express the total energy. The Hamiltonian is the sum of the kinetic energy (KE), ![]() , and
the potential energy (PE),
, and
the potential energy (PE), ![]() .
.
H = KE + PE = KE + |
|
|
|
|
(C-17) |
| with | |
|
|
| and | |
|
|
| For our two-body 3 molecule system, | |
|
(C-18) |
![]() is the potential energy surface. We only need to specify two distances (e.g. RAB, RBC) because the other is then a fixed quantity.
is the potential energy surface. We only need to specify two distances (e.g. RAB, RBC) because the other is then a fixed quantity.
The distances RAB and
RBC are shown in the potential energy surface ![]() (RAB, RBC) in Figure PRS.3C-5 along with the trajectory of the reaction.
(RAB, RBC) in Figure PRS.3C-5 along with the trajectory of the reaction.
|
|
Side view along the trajectory |
|
Figure PRS.3C-5 Reactant coordinates and the potential energy surface.
A summary of the above equations used to solve for the molecular trajectories is shown in Table PRS.3C-3.
Table PRS.3C-2 Equations to be solved to predict the trajectories
| [To get an idea where this
eqn. comes from, recall for the A molecule |
|
||
| For j = 1, 2, 3 | ||
| (A) |
|
|
| For j = 4, 5, 6 | ||
| (B) |
|
|
| (C) |
|
|
| (D) |
|
|
These equations are analogous to the Px and x,y,z equations shown on pages 3 and 4.
The above equations can be solved simultaneously using a software package. To predict the location Qi, from which one can determine the molecular distances, E.g., RBC, RAB. However, before we begin to do this we need to specify the parameter values and the initial conditions.
| To map out the molecular trajectories to determine if a reaction has occurred we need three things. | |||
| 1. | The Governing Equations. These equations are given in Table PRS.3C-2. | ||
| 2. | The specified values of the variables. These values fall in two categories and are shown in Table PRS.3C-3. | ||
| (a) | Those variables to be studied to learn their effect on the reaction rate. These are the specified variables. | ||
| (b) | Those variables whose numerical values are specified by the Monte Carlo . | ||
| 3. | The initial values to calculate the molecular trajectories. The initial parameter values are given in Table PRS.3C-4 and corresponds to the orientation of the A and BC molecules shown in Figure PRS.3C-6. | ||
Table PRS.3C-3 Categories of Variable Parameter Values
(1) Specified and Given a Numerical Value
(a) Initial Relative Velocity, UR
(b) Impact Parameter, b
(c) Vibrational Quantum Number, ν
(d) Rotational Quantum Number, J
(2) Chosen by the Monte Carlo Simulation
(a) Distance between the B and the C molecule, RBC (R-<RBC<R+)
(b) Orientation of BC relative to A specified by angles θ (0<θ<π) and Φ (0<Φ<2π) (See Figure PRS.3C-6).
(c) Internal angular momentum of H2 molecule specified by an angle η (i.e., which direction it is rotating).
We are going to choose our coordinate system such that molecule A and the center of mass of BC lie the y-z plane and that A approaches BC along the z axis.
Table PRS.3C-4 Initial Conditions to Start the Trajectory
Initial Conditions
Specified Initial Conditions, ro, b, ν, J
The following variables are chosen randomly: RBC, Φ,θ, and η
| Location of C wrt B | Angular momentum of B-C | |
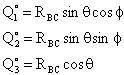 |
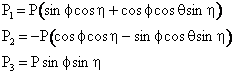 |
|
| where† |
||
| The center of mass lies in x-y plane. Location of A wrt center of mass of B-C | ||
 |
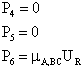 |
|
with ro the initial distance between A and the center of mass of BC
Here ![]() is
Plank's constant divided by 2π and R+ is the turning
point radius shown in Figure PRS.3C-7. The value of ro is chosen as small as possible to save computing time but not so small as to experience any potential interactions
between the A and BC molecules. A schematic of the initial conditions
and the orientation is shown below in Figure PRS.3C-6.
is
Plank's constant divided by 2π and R+ is the turning
point radius shown in Figure PRS.3C-7. The value of ro is chosen as small as possible to save computing time but not so small as to experience any potential interactions
between the A and BC molecules. A schematic of the initial conditions
and the orientation is shown below in Figure PRS.3C-6.
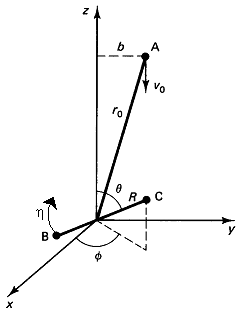
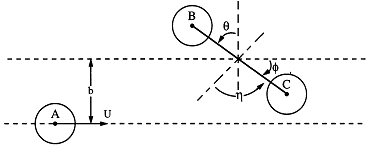
Figure PRS.3C-6 Reactive trajectory. Courtesy of J. I. Steinfeld, J. S. Francisco, W. L. Hose,Chemical Kinetics and Dynamics, p.264, Prentice Hall, Upper Saddle River, New Jersey (1989) with v0 = U = UR in our notation)
BC, between the B and the C molecule.

![]()
Figure PRS.3C-7 Turning points of H-H vibration.
The distance R cannot take on any value, it can only between the maximum and minimum points of the vibration, R±. That is
R- ≤ R ≤ R+
We calculate the values R- and R+ by knowing at the turning points where the oscillation changes direction and R+ and R- where all the vibration energy is potential vibrational energy. That is, the molecules are in their most compressed state, R-, or their most extended state R+. The potential energy is given by a Morse function DBC [1 - exp [- βBC(R-Re)]2 where βBC, DBC and Re are the appropriate values for H2. The quantum mechanical energy for the BC molecule in the νand J quantum state is Equation 15 of Karplus† article is
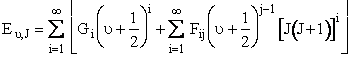
(C-19)
The constants in this equation (e.g. G1, I11, etc.) are given for H2 in Table I in Karplus. By equating equations (C-19) and (C-20) we can find the roots of the equation for R to determine the turning points, (R+ and R-). There is no angular momentum along the bond direction.
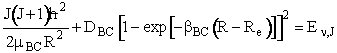
(C-20)
This calculation is tedious and difficult so we just need to accept that we can find the roots and "move on". Figures PRS.3C-8, and PRS.3C-9 show the results of the calculations we just outlined.
|
|
|
|
| Figure PRS.3C-8 Non Reactive Trajectories |
Figure PRS.3C-9 Reactive Trajectories |
|
Figures PRS.3C-8 and PRS.3C-9, Courtesy of ACS, Karplus, M., R.N. Porter, and R. D. Sharma, J of Chemical Physics, 43, p3259
| Figure 8 |
Figure 9 |
|||||||
| (a) |
(b) |
(c) |
(a) |
(b) |
(c) |
|||
|
|
1.32 |
1.96 |
1.18 |
1.32 |
1.96 |
1.18 |
||
| J |
0 |
2 |
5 |
0 |
2 |
5 |
||
|
|
0 |
0 |
0 |
0 |
0 |
0 |
||
One notes from Figures PRS.3C-8 (b) and (c) that the B-C molecule is rotating as evidenced by the fact that the RAB and RAC trajectories cross. On the other hand for the case of no rotation, J=0 in Figure (a), they do not cross. By the two crossings of RAB and RAC in Figure 8 (c) , one observes a faster rotation speed, than Figure 8(a) where J=2. In Figure PRS.3C-9 (a) we see that while B-C is not rotating before reaction, the AC molecule is rotating after reaction as evidenced by the crossing of the RAC and RBC trajectories. The time of the trajectory calculation is 4-8x10-14s, the ν=0 vibration period is 0.5x10-14s, the rotational period for J=1 is 20x10-14s and for an any quantum number J is [27x10-14/J[(J+1)]1/2]s.
For a specified set of conditions, we now simply run a simulation and see whether or not a reaction occurs. Then we repeat for the same specified conditions but different Monte Carlo chosen values. A number of trajectories were calculated for the specified parameters [VR, J, ν, b] using Monte Carlo techniques to calculate many trajectories similar to those shown in Figures PRS.3C-8 and PRS.3C-9. We keep track of the number of trajectories (simulations) that react, NR, and those that don't react. We then take the ratio of those trajectories that resulted in reaction to all the trajectories carried, N, out to calculate the reaction probability.
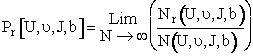
(C-21)
Where N is the total number of trajectories calculated and Nr is the number that resulted in reaction. We sum the AB reactions and AC reaction to get Nr.
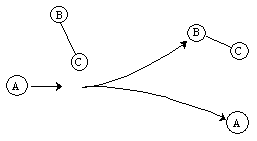

Reaction
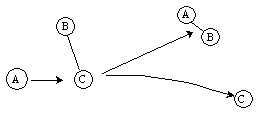

Figure PRS.3C-10 Molecular Trajectories.
Now vary one of the specified parameters by running a number of Monte Carlo simulations for each value of that parameter. First b was varied while holding U, ν, and J constant. A number of simulations (trajectories) are carried out for each value of b in order to calculate Pr at that value of b. Then b is increased and the simulations repeated to again calculate Pr at another value of b. The results of the calculation are shown in Figure PRS.3C-11. For two different velocities. One notes that even for head-on collision (b=0) the probability is not 1.0, due to orientation effects and that the offset impact parameter, b, of A relative to the center of mass of BC is greater than 1.85 au, then no reaction will occur.
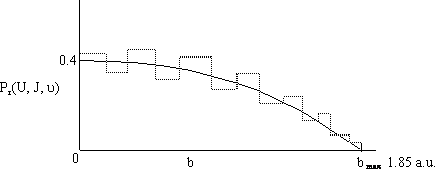
Figure PRS.3C-11 Probability of reaction as a function of the impact parameter.
[Note 1 a.u. = 59.9 pm and 1 hartree (htr) = 627 kcal]
The dashed lines represent the actual calculated values of Pr while the curve represents the smoothed values. We note there is a maximum value of the impact parameter, bmax, above which no reaction will take place.
The reaction cross section, Sr is the probability of reaction, Pr and the cross section πb2. In differential form Sr is a function of the relative velocity and the rotational and vibrational quantum numbers ν and J.
|
|
where b goes between zero and bmax
|
We are going to make an approximation to simplify the calculations. The approximation is that the curve in Figure PRS.3C-11 can be approximated by a cosine function, namely
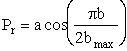
(C-23)
Both a and bmax increase with increasing velocity as shown in Table PRS.3C-5.
Table PRS.3C-5
| U (cm/s x 106) |
a |
bmax (a.u.) |
|||
| 0.78 |
0 |
0 |
|||
| 0.93 |
0.26 |
0.95 |
|||
| 1.17 |
0.39 |
1.85 |
|||
| 1.32 |
0.42 |
2.00 |
|||
| 1.95 |
0.61 |
2.50 |
For the curve shown for UR = 1.17x106 cm/s in Figure PRS.3-11
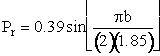
r as a function of b for each U. Using the cosine approximation, Eqn. (C-23) we can determine a and bmax for the chosen value of U. The reaction smoothed probability is shown as a function b for two different relative velocities in Figure PRS.3C-12

Figure PRS.3C-12 Reaction probability as a function of impact parameter for two different relative velocities
We need to specify the vibration and rotation energies, i.e., quantum number, ν and J when carrying out these calculations.
From Figure PRS.3C-12 we see as the velocity increases to 1.95 cm/s both a and bmax increase. Substituting for Pr using Equation (C-23) into Equation (C-22) we
![]()
Let
![]()
Substituting for b and for db
![]()
Integrating by parts
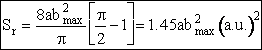
(C-24)
The reaction cross section Sr(U,J,ν) can now be found as a function of the relative velocity for which one can determine the corresponding relative transition energy, ER
![]()
Equation (C-24) can be used to calculate the reaction cross section at any relative velocity. For example, when UR = 1.17x106 cm/s, a = 0.39, and b = 1.85 a.u., then
when, ![]() , then
, then
![]()
We continue in this manner to choose U, vary b and find Pr as a function of b to obtain a and bmax to arrive at Figure PRS.3C-12. One notes from this figure that while the cross section at UR = 1.17x106 cm/s for which Sr = 1.94 (a.u.)2 agrees with the simulation. The value at U = 1.95x106 cm/s of Sr = 4.4 (a.u.)2 is different than the value of 5.45 (a.u.)2 just calculated. The reason for this discrepancy is that we used the cosine function to approximate the Pr very b curve rather than say fitting (Pr vs. b) with a polynomial or plotting the "data" as bPr as a function b and multiply the area under the curve by 2π to get Sr.
![]()
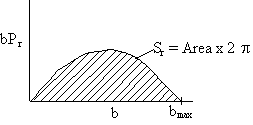
Figure PRS.3C-13
this technique while more tedious and labor intensive will give a more accurate value than the cosine approximation.

Figure
PRS.3C-14 Reaction cross
section as a function of relative velocity. Here 1 atomic unit ≡
1 a.u. = 0.59 Å = 59 pm![]() = (1 a.u)2
= (1 a.u)2
We note Sr ≡ 0
until we reach ![]() .† This energy is threshold
kinetic energy necessary for the molecules A and BC to react. If the
relative velocity U is such that the threshold energy is not exceeded,
no reaction will occur. Now let's look at the effect of some of the
parameters, namely
.† This energy is threshold
kinetic energy necessary for the molecules A and BC to react. If the
relative velocity U is such that the threshold energy is not exceeded,
no reaction will occur. Now let's look at the effect of some of the
parameters, namely ![]() and J,
on the reaction cross section.
and J,
on the reaction cross section.
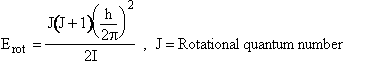
(C-25)
I = moment of inertia
We now carryout a number of realizations and marking down those runs that result in reaction (e.g.,
Figure PRS.3C-9) and those that do not result in reaction (e.g.,
Figure PRS.3C-8) to arrive at Figure PRS.3C-11. Figure
PRS.3C-14 shows the results of the calculations that give the
reaction cross section as a function of relative velocity (kinetic
energy ![]() )
for the case J=0 and
)
for the case J=0 and ![]() =0.
=0.
Now lets change J and vary U (i.e., ER) to calculate the reaction cross section
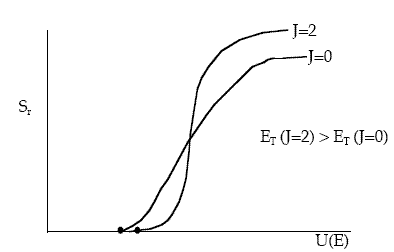
Figure PRS.3C-15 Effect of rotation quantum number on reaction cross section.
We see that both the threshold kinetic energy, ET, and the limiting cross section at high kinetic energies increase with increasing rotation quantum number (frequency) For J=2, the rotation period is 11.1x10-14s compared with the interaction time of 10-14s. At low kinetic energies the increased rotational energy makes it more difficult to react (steric effects). Also at higher kinetic energies the increased rotational energy increases the reaction cross section. However, the rotational energy is not available for crossing the potential energy barrier, V(RAB, RBC, RAC).
Vibrational Energy
The vibrational energy is†
![]()
(C-26)
ν= vibrational quantum number, v0 is the frequency of vibration, and h is Plank's constant.
Zero point energy ν=0
![]()
The vibrational energy contributes to the kinetic to supply the energy to pass over the barrier. However, not all the vibrational energy is available for reaction. Now lets change ν and vary U, (i.e., ER) and calculate the reaction cross section as shown in Figure PRS.3C-16
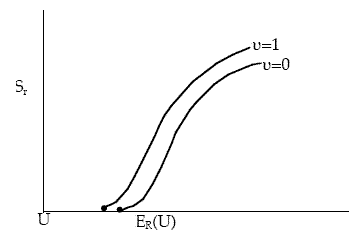
Figure PRS.3C-16 Effect of vibrational quantum number on reaction cross section.
At higher vibrational states the threshold energy decreases while the limiting value of Sr increases. However, Karplus notes that too few vibrational states were simulated to reach a definitive conclusion.
Figure PRS.3C-17 shows the reaction cross as a function of kinetic energy for the hard sphere and line of center models along with the results of molecular dynamics calculations.

Figure PRS.3C-17 Comparison of models.
A discussion of the reaction cross section for the rigid sphere model and for line of centers model is given in Professional Reference Shelf 3A. We see the molecular dynamics (M.D.) trajectory for ν=0 and J=0 gives a reaction cross section that falls between these two models.
Knowing the reaction cross section we can
now proceed to calculate the overall rate of reaction, -rA. The differential rate of reaction d[-rA(J,ν)]
of species A, which has a velocity VA
and a concentration d![]() >A,
with species BC, which has a concentration of d
>A,
with species BC, which has a concentration of d![]() BC
that has velocity VB
and is the ν
vibrational state and the J rotational state, is
BC
that has velocity VB
and is the ν
vibrational state and the J rotational state, is
![]()
(C-27)
(mole A/s/dm3)
where
| -rA(J, ν) |
= |
Rate of reaction of A with BC molecules in the J rotational state and ν vibrational state. (mol A/dm3/s) |
|
| U |
= |
Relative velocity |
|
| d |
= |
Concentration of A molecules with velocities between VA and |
. |
| = |
|
||
| CA |
= |
The total concentration of A molecules (mol A/dm3) |
|
| f(VA) |
= |
Distribution of molecular velocities of molecule A. The distribution function is similar for BC molecules BC (c.f. Eqn. (C-27)). |
|
| d |
= |
Concentration of BC molecules with rotational state J, vibrational state ν,
and velocities between VBC and |
|
| d |
= |
|
|
|
|
= | ||
| CBC |
= |
The total concentration of all B-C molecules (mol/dm3), and |
|
| FBC(J, |
= |
The fraction of B-C molecules in the J rotational state and the |
|
The distribution functions in the above equations are for velocity 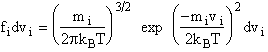 for rotation and vibration
where and the values of Gi and Fi are given in Karplus' article. [Note: also see Ch.12 Laidler pp.449-458.]†> |
(C-28)
(C-29)
(C-30)
|
Calculating the Total Rate
First we integrate Equation(C-27) overall all velocities so that
velocity is incorporated in the rate and it is now only a function
![]() and J.
and J.
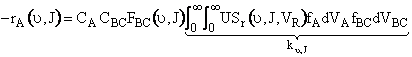 |
(C-31) |
| (C-32) |
The rate, ![]() ,
Eqn (C-32), is only for those reactions with vibrational
,
Eqn (C-32), is only for those reactions with vibrational ![]() and rotation states J. The total rate of reaction is found by
summing overall vibrational and rotational states
and rotation states J. The total rate of reaction is found by
summing overall vibrational and rotational states
| (C-33) | |
| (C-34) | |
| (C-35) |
A comparison of the theoretical and calculate values of the specific reaction rate are shown in Table PRS.3C-6.
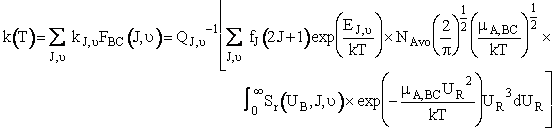 (C-36)
(C-36)
Equation (C-36) is Eqn. 41 in Karplus' article.† Where NAvo is Avogadros number.
After carrying out the Monte Carlo
Simulations for all specified variables b, U (i.e., EAC),
J and ![]() at a given temperature
we use Equation (C-36) to calculate the specific rate k(T) next.
The temperature was changed (e.g., from 300 to 500K) and the specific
reaction rate recalculated. The results of some of these of the
calculations are shown in Table PRS.3C-6.
at a given temperature
we use Equation (C-36) to calculate the specific rate k(T) next.
The temperature was changed (e.g., from 300 to 500K) and the specific
reaction rate recalculated. The results of some of these of the
calculations are shown in Table PRS.3C-6.
Table PRS.3C-6 k(T) Values from M.D. calculations and experiment.a,h
| T(K) |
k(T) x 10-11 |
k(T) x 10-11 |
k(T) x 10-11 |
| 300 |
0.0018 |
0.002008 |
0.0014-0.0020 d |
| 500 |
0.225 |
0.23 |
. . . |
| 700 |
2.01 |
2.04 |
2.49-4.99 e,g |
| 900 |
7.3 |
7.38 |
7.6-15.2 f,g |
| 1000 |
11.69 |
11.78 |
11.0-22.0 f,g |
a All values of k(T) is units of cubic centimeters per mole•second.
b Calculated by Eq. (41) with Sr given by Eq. (43) and Table II of Karplus' paper.
c Calculated by Eq. (C-36) with computed values of Sr.
d K. Geib and P. Harteck, Z. Physik Chem. Bodenstein Fastband 849(1931).
e M. van Meersche, Bull. Soc. Chim. Belges 60, 99 (1951).
f A. Farkas and L. Farkas, Proc. Roy. Soc. (London) A152, 124 (1935).
g G. Boato, G. Careri, A. Cimino, E. Molinari, and G. G. Volpi, J. Cl. Phys. 24, 783 (1956) have suggested that the values of van Meersche and Farkas and Farkas should be multiplied by 0.5 to correct for the present oxygen in the reaction mixture. Since this point has not been settled unequivocally, we list the range corresponding to 0.5 times the measured value to measured value.
h Table PRS.3C-6 Courtesy of ACS, Karplus, lit.cit.
Looking at the specific reaction rates k in Table PRS.3C-6 we see
| Theory |
Experiment |
||
| T = 300 |
k = 0.00185 cm3/s•mol |
0.0017-006 cm3/s•mol |
|
| T = 1000 |
k = 11.5 cm3/s•mol |
11-22 cm3/s•mol |
We can use the theoretical values
of k(T) predicted in Table PRS.3C-2 to determine the activation
energy. A plot of ln k vs. 1/T is shown in Figure
PRS.3C-17.
Figure PRS.3C-18 Using molecular dynamics to predict activation energy.(From Karplus, et.al, J.Chem. Phys. 43, p3259 (1965))
From the slope we find EA = 7.4 kcal/mole.
with
which is in excellent agreement with the experimental values.
A plot of the values in Table PRS.C3-5 in the form of ln k(T) vs. 1/T will yield an activation energy of 7.4 kcal/mol which is very close to the experimental value, of 7.5 kcal/mol. We see there is excellent agreement of both the frequency factor A and the activation energy EA between the theory and experiment. We also note the differences is the values of the following energies.
A summary of all the energies obtained from the literature or by calculation are given in Figure PRS.3C-19.

Figure PRS.3C-19 Comparison of Energies
The barrier height = 9.2 kcal
The minimum kinetic energy (MKE) = 5.7 kcal
The ground state vibrational energy (GSV) = 6.2 kcal
The ground state vibration energy + MKE = 6.2 + 5.89 = 11.89 kcal
The activation energy = 7.5 kcal
One notes that the activation energy is less than the barrier height which is a result of quantum mechanical tunneling. One also notes that not all the ground state vibrational energy is available to be added to the translational energy to cross the energy barrier.
Problems for Molecular Dynamics
The equation of motion for molecules A and BC were coupled with potential energy surface to calculate trajectories of the A and BC molecules. The reaction probability was calculated by counting up the number of trajectories that resulted in reaction and dividing by all the trajectory trials. Below a threshold value of the translational kinetic energy no reaction occurs. There is also a maximum value of the impact parameter above which no reaction will occur. Owing to steric effects. The reaction probability only reaches a value of 0.6 even for heard on collisions (b-0) and very large translational kinetic energies. The reaction cross can be calculated from the impact parameter and relative velocity for given values of the vibrational and rotational quantum numbers. It was found to have a sigmodal shape, increasing as the kinetic energy (velocity) increased. The threshold kinetic energy decreased with increasing vibration quantum numbers and increased with increasing rotational quantum numbers.
The characteristic times are the rotational vibrational period for J=1 is, 19x10-4s and for J=5 is 4.9x10-14s, the vibration period is 0.5x10-14s, the time of interaction is 10-14s and the time of the trajectory calculation is between 4 and 8x10-14s. We note that the rotational period is an order of magnitude greater than the interaction time, while the vibrational period is the same order as the interaction time.
The minimum kinetic energy 5.69 kcal is not sufficient
to cross the potential energy barrier of 9.13 kcal and requires
some of the vibrational energy from the BC molecules. The sum
of the threshold (i.e., minimum energy necessary for reaction)
5.69 kcal and the ![]() =0
vibrational state energy of 6.2 kcal gives a total energy of
11.89 kcal which is greater than barrier height of 9.13 kcal.
The difference between 11.89 and 9.13 indicates not all the
vibrational energy is available for reaction. None of the rotational
energy is available for reaction.
=0
vibrational state energy of 6.2 kcal gives a total energy of
11.89 kcal which is greater than barrier height of 9.13 kcal.
The difference between 11.89 and 9.13 indicates not all the
vibrational energy is available for reaction. None of the rotational
energy is available for reaction.
The rate constants k(T) were calculated as a function of temperature from first principles with no adjustable parameters. When the ln k was plotted as function of 1/T the activation energy was found to be 7.4 kcal/mol which is in excellent agreement with the experimental value of 7.5 kcal/mol. The fact that the activation energy is smaller than barrier is a consequence of quantum mechanical tunneling.
Karplus, M, P.N. Porter, and R. D. Sharma, J. of Chemical Physics, 43, 9, p.3259 (1965).
Laidler, K. J., Chemical Kinetics, 3rd ed., Harper Collins, New York, 1987.
Steinfeld, J. I., J. S. Francisco, and W. L. Hase, Chemical Kinetics and Dynamics, Prentice Hall, Upper Saddle River, NJ, 1989 (see Ch.8, p.246-268).
† Karplus, M., R.N. Porter, and R. D. Sharma, Journal of Chemical Physics, 43, 9, p.3259 (1965).
† Steinfeld, J.I., J.S. Francisco, and W. L. Hase, Chemical Kinetics and Dynamics, Prentice Hall, Englewood Cliffs, NJ (1989).
† Steinfeld
Lit.Cit. for ![]() see
p264.
see
p264.
† Steinfeld, Lit cit p265.
† Karplus, Lit cit
† Karplus, Lit cit.
† See most any Physical Chemistry textbook, e.g., Atkins, P.A. Physical Chemistry 6th Ed. W. H. Freemand & Co. NY (1997).
† Karplus, Lit cit, also see Laidler Lit cit p449-558.
† Karplus, Lit cit