To show
| (A12) |
Again we solve the wave equation for two molecules undergoing oscillation about an equilibrium position x = 0. The potential energy is shown below as a function of the displacement from the equilibrium position x = 017
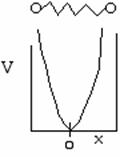
The uncertainty principle says that we cannot know exactly where the particle is located. Therefore zero frequency of vibration in the ground state, i.e. ν = 0 is not an option18. When ν0 is the frequency of vibration, the ground state energy is
| (V1) | |||||
| Harmonic oscillator 19 | |||||
| Spring Force |
|||||
| the solution is of the form for t=0 then x=0 | |||||
| where | |||||
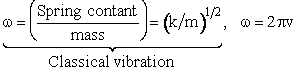 |
|||||
| The potential energy is | |||||
| (V2) | |||||
| We now want to show | |||||
| (V3) | |||||
| We now solve the wave equation: | |||||
| (V4) | |||||
| to find the allowable energies, ε. | |||||
Let 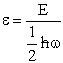 , where , where 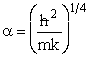 , , |
|||||
| With these changes of variables Eqn. (A15) becomes | |||||
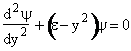 |
(V5) | ||||
| The solutions to this equation20 will go to infinity unless | |||||
| [c = speed of light]21 | |||||
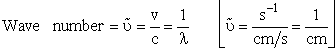 |
|||||
| (V6) | |||||
| Measuring energy relative to the zero point vibration frequency, (i.e., ν = 0) gives | |||||
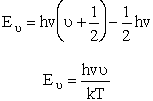 |
|||||
| Substituting for |
|||||
 |
|||||
|
(V7) | ||||
| For |
|||||
| (V8) | |||||
| For m multiple frequencies of vibration | |||||
| Order of Magnitude and Representative Values | |||||
| For H2O
we have three vibrational frequencies with corresponding wave numbers, |
|||||
| and | |||||
17P. W. Atkins, Physical Chemistry, 5th ed. (New York: Freeman, 1994), p. 402.
18 P. W. Atkins, Physical Chemistry, 5th ed. (New York: Freeman, 1994), pp. 22, 402.
19P. W. Atkins, Physical Chemistry, 5th ed. (New York: Freeman, 1994), p. 402.
20P. W. Atkins, Physical Chemistry, 5th ed. (New York: Freeman, 1994), p. 22, Appendix 8.
Return to Transition State Theory