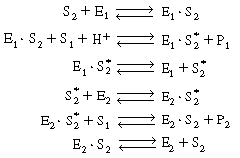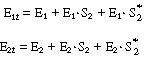|
|
|
R9.6.1: Microbial Growth on Multiple Substrates
Microbial Growth on Multiple Substrates
|
|
|
|
|
|
|
|
|
|
R9.6.2 Enzyme Regeneration
|
|
|
|
|
As a first example we shall consider the oxidation of glucose (Sr
) with the aid of the enzyme glucose oxidase [represented as either G.O.
or (Eo )] to give 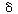 -gluconolactone
(P): -gluconolactone
(P):

|
|
|
|
|
In this reaction, the reduced form of glucose oxidase (G.O.H2
), which will be represented by Er
, cannot catalyze further reactions until it is oxidized back to Eo
. This oxidation is usually carried out by adding molecular oxygen to
the system so that glucose oxidase, Eo
, is regenerated. Hydrogen peroxide is also produced in this oxidation
regeneration step.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Overall, the reaction is written |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
In biochemistry texts, reactions of this type involving regeneration are usually
written in the form
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
The reaction is believed to proceed by the following sequence
of elementary reactions: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
We shall assume that reaction involving the dissociation
between reduced glucose oxidase and -lactone
is rate limiting. The rate of formation of -lactone
is rate limiting. The rate of formation of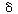 -lactone
(P1 ) is given by the equation -lactone
(P1 ) is given by the equation |
|
|
|
|
|
|
|
|
|
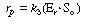
|
(R7.4-1)
|
|
|
|
|
|
|
|
|
After applying the pseudo-steady-state hypothesis to the rates of
formation of
(Eo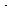 Sr ), (Er
Sr ), (Er So ), and (Er
),
So ), and (Er
), |
|
|
|
|
|
|
|
|
|
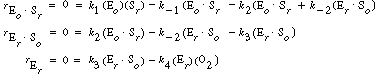
|
|
|
|
|
|
|
|
|
|
we can solve for the following concentrations of the active
intermediates in terms of the concentrations of glucose, oxygen, and unbound
oxidized enzyme. |
|
|
|
|
|
|
|
|
|
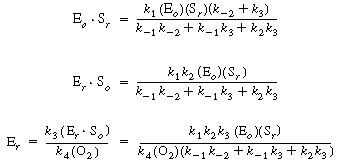
|
(R7.4-2)
(R7.4-3)
(R7.4-4)
|
|
|
|
|
|
|
|
|
After substituting Equation (R7.4-3) into Equation (R7.4-1),
the rate law is written as |
|
|
|
|
|
|
|
|
|
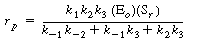
|
(R7.4-5)
|
|
|
|
|
|
|
|
|
The total enzyme initially present is given by the sum |
|
|
|
|
|
|
|
|
|
(Et ) = (Eo
) + (Eo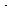 Sr
) + (Er Sr
) + (Er So
) + (Er ) So
) + (Er )
|
(R7.4-6)
|
|
|
|
|
|
|
|
|
After using Equations (R7.4-2), (R7.4-3), and (R7.4-4) to
substitute for the active intermediate in Equation (R7.4-6), one can then
solve for the unbound oxidized enzyme concentration, Eo
, and substitute it into Equation (R7.4-5) to obtain the form of the rate
law |
|
|
|
|
|
|
|
|
|
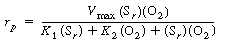
|
(R7.4-7)
|
|
|
|
|
|
|
|
|
Example R9.6-1
Construct a Lineweaver-Burk Plot for Different Oxygen Concentrations
|
|
|
|
|
|
|
|
|
|
The reaction above illustrates how an enzyme can be regenerated
through the addition of another substrate, in this case O2
. |
|
|
|
|
|
|
|
|
|
R9.6.3 Enzyme Cofactors
|
|
|
|
|
|
|
|
|
|
In many enzymatic reactions, and in particular biological
reactions, a second substrate (i.e., species) must be introduced to activate
the enzyme. This substrate, which is referred to as a cofactor or
coenzyme even though it is not an enzyme as such, attaches to the
enzyme and is most often either reduced or oxidized during the course of
the reaction. The enzyme-cofactor complex is referred to as a holoenzyme.
An example of the type of system in which a cofactor is used is the formation
of ethanol from acetaldehyde in the presence of the enzyme alcohol dehydrogenase
(ADH) and the cofactor nicotinamide adenine dinucleotide (NAD). After the
enzyme is activated by combination with the cofactor in its reduced state,
NADH, |
|
|
|
|
|
|
|
|
|
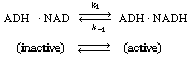
|
|
|
|
|
|
|
|
|
|
the holoenzyme (ADH NADH) reacts
with acetaldehyde in acid solution to produce ethanol and the oxidized form of the
enzyme-cofactor coupling NADH) reacts
with acetaldehyde in acid solution to produce ethanol and the oxidized form of the
enzyme-cofactor coupling
(ADH NAD+
): NAD+
): |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
The inactive form of the enzyme-cofactor complex for a specific
reaction and reaction direction is called an apoenzyme. This reaction
is followed by dissociation of the apoenzyme (ADH NAD+
), which is usually relatively slow. NAD+
), which is usually relatively slow. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
The values of the specific rates are3
: |
|
|
|
|
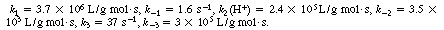
|
|
|
|
|
|
|
|
|
|
Typical initial concentrations for a small laboratory batch reactor
experiment might be
[acetaldehyde]0 = 10-1 mol/L, [ADH]0 = 10-7 g mol/L, and [NADH]0 = 10-4 g mol/L. The overall reaction is often written in the form
alcohol dehydrogenase
|
|
|
|
|
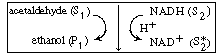
|
|
|
|
|
|
|
|
|
|
The ADH enzyme molecule produced by the dissociation of (ADH NAD+
) can participate in subsequent reactions involving the formation of ethanol,
while the nicotinamide adenine dinucleotide from the dissociation cannot
participate until it is reduced back to NADH. Since the initial concentration
of NADH is usually several orders of magnitude greater than the initial
concentration of enzyme, the consumption of NADH will not limit the overall
rate of formation of ethanol nearly so much as the slow dissociation of
the (ADH NAD+
) can participate in subsequent reactions involving the formation of ethanol,
while the nicotinamide adenine dinucleotide from the dissociation cannot
participate until it is reduced back to NADH. Since the initial concentration
of NADH is usually several orders of magnitude greater than the initial
concentration of enzyme, the consumption of NADH will not limit the overall
rate of formation of ethanol nearly so much as the slow dissociation of
the (ADH NAD+
) complex. This apoenzyme essentially ties up the enzyme, preventing it
from becoming free (unbound) to combine with NADH to form the holoenzyme,
which reacts with acetaldehyde to produce ethanol. We note that the reaction
rate might be increased considerably if we had a way of going directly from
(ADH NAD+
) complex. This apoenzyme essentially ties up the enzyme, preventing it
from becoming free (unbound) to combine with NADH to form the holoenzyme,
which reacts with acetaldehyde to produce ethanol. We note that the reaction
rate might be increased considerably if we had a way of going directly from
(ADH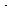 NAD+
) to (ADH NAD+
) to (ADH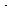 NADH);
that is, NADH);
that is, |
|
|
|
|
|
|
|
|
|
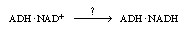
|
|
|
|
|
|
|
|
|
|
rather than having the enzyme ADH go through the steps of
dissociating from |
|
|
|
|
|
|
|
|
|
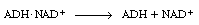
|
|
|
|
|
|
|
|
|
|
and then combining with NADH: |
|
|
|
|
|
|
|
|
|
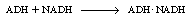
|
|
|
|
|
|
|
|
|
|
Example R9.6-2
Derive an Initial Rate Law for Alcohol Dehydrogenase
|
|
|
|
|
|
|
|
|
|
Equation (RE7.4-1) is of a form
that is often used in the interpretation of initial rate data for enzymatic
reactions involving two substrates. The parameters K12
, K1 , K2
, and Vmax in Equation (RE7.4-1),
which was first developed by Dalziel,4
may be evaluated through a series of Lineweaver-Burk plots. After substituting
the numerical values for K1
, K2 , K12
and recalling the initial concentrations specified (S1,0
= 0.1 g mol/L, S2,0 = 10-4
g mol/L), we see that we can neglect K12
and K2 (S2
) with respect to the other terms in the denominator, in which case Equation
(G25-7) becomes |
|
|
|
|
|
|
|
|
|
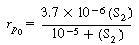
|
(R7.4-8)
|
|
|
|
|
|
|
|
|
The initial rate is rp 0
= 3.7 x 10-6 g mol/L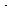 s.
In the next section we compare the preceding rate with one in which a third
substrate is added to the system. s.
In the next section we compare the preceding rate with one in which a third
substrate is added to the system. |
|
|
|
|
|
|
|
|
|
R9.6.4 Multiple-Substrate Systems
In the preceding section we stated that the rate of formation of ethanol
might be increased if the (ADH NAD1
) complex could be converted by some means directly to the enzyme-cofactor
complex (ADH NAD1
) complex could be converted by some means directly to the enzyme-cofactor
complex (ADH NADH)
without having the enzyme ADH go through a series of reactions. This can
be achieved by the addition of a third substrate, S3
, (e.g., propanediol), which during reaction (to form DL-lactaldehyde)
will also regenerate the cofactor (NADH). The overall reaction sequence
for this case is NADH)
without having the enzyme ADH go through a series of reactions. This can
be achieved by the addition of a third substrate, S3
, (e.g., propanediol), which during reaction (to form DL-lactaldehyde)
will also regenerate the cofactor (NADH). The overall reaction sequence
for this case is
|
|
|
|
|
|
|
|
|
|
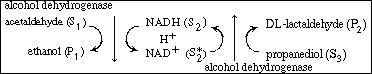
|
|
|
|
|
|
|
|
|
|
As a first approximation, this sequence of reactions could
be represented by the following elementary steps: |
|
|
|
|
|
|
|
|
|
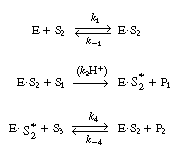
|
|
|
|
|
|
|
|
|
|
Example R9.6-3
Derive a Rate Law for a Multiple Substrate System
This same reaction has been carried in the reverse direction
by Gupta and Robinson.5
They measured the initial rate of conversion of DL-lactaldehyde to propanediol
in the presence of NAD 1 and ADH. The
rate of dissociation of the enzyme-cofactor complex (ADH NADH)
is believed to be rate limiting. This is con- firmed by the fact that
when ethanol was added to the system, the reaction rate increased 100-fold
by having the ethanol convert the (ADH NADH)
is believed to be rate limiting. This is con- firmed by the fact that
when ethanol was added to the system, the reaction rate increased 100-fold
by having the ethanol convert the (ADH NADH)
directly back to (ADH NADH)
directly back to (ADH NAD+
). NAD+
).
Example R9.6-4
Calculate the Initial Rate of Formation of Ethanol in the Presence of Propanediol
|
|
|
|
|
|
|
|
|
|
In analyzing multiple reactions in this manner, one should always
question the validity of the application of the PSSH to the various active intermediates.
Since the nicotinamide adenine dinucleotide is continually regenerated and
the total concentration of the cofactor (in its oxidized, reduced,
bound, and unbound forms) remains constant throughout the
course of the reaction, it might be desirable to replace S2
in the rate law in terms of the total cofactor concentration, S
t . Neglecting any unbound, the total (initial) cofactor
concentration is |
|
|
|
|
|
|
|
|
|
|
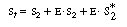
|
(R7.4-9)
|
|
|
|
|
|
|
|
|
The total concentration of enzyme is |
|
|
|
|
|
|
|
|
|
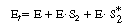
|
(R7.4-10)
|
|
|
|
|
|
|
|
|
Subtracting Equation (R7.4-9) from Equation (R7.4-10), we
obtain |
|
|
|
|
|
|
|
|
|
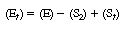
|
(R7.4-11)
|
|
|
|
|
|
|
|
|
Equation (R7.4-11) can be rewritten in the form |
|
|
|
|
|
|
|
|
|
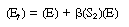
|
(R7.4-11)
|
|
|
|
where
|
|
|
|
|
|
|
|
|
|
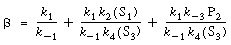
|
(R7.4-12)
|
|
|
|
|
|
|
|
After adding Equations (R7.4-11) and (R7.4-12) and rearranging,
we obtain |
|
|
|
|
|
|
|
|
|
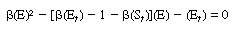
|
(R7.4-13)
|
|
|
|
|
|
|
|
|
which is solved for the unbound enzyme concentration
in terms of S1 , S3
, P2 , Et
, and St . |
|
|
|
|
|
|
|
|
|

|
(R7.4-14)
|
|
|
|
|
|
|
|
|
We can substitute Equation (R7.4-14) into (R7.4-9) and rearrange to determine the concentration of the unbound cofactor in its reduced form, that is, |
|
|
|
|
|
|
|
|
|
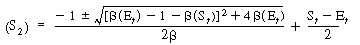
|
(R7.4-15)
|
|
|
|
|
|
|
|
|
The rate law was given by |
|
|
|
|
|
|
|
|
|
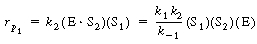
|
(R7.4-16) |
|
|
|
|
|
|
|
|
One could substitute Equations (R7.4-14) and (R7.4-15) for
S2 and E into Equation (R7.4-16) to arrive
at a reasonably complicated rate law involving S1
, St , S 3
, P2 , and Et
. However, a computer solution would be used in most reaction sequences
that are this involved algebraically, in which case further substitution
would not be necessary and one could use Equations (R7.4-14), (R7.4-15), and
(R7.4-16) directly. |
|
|
|
|
|
|
|
|
|
|
|
|
|
R9.6.5 Multiple Enzymes Systems
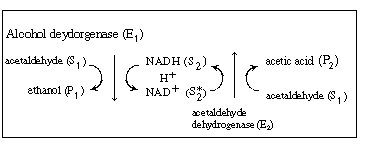
We shall again consider the production of ethanol from
acetaldehyde which uses the cofactor NADH. However, the regeneration of
NAD+ to NADH is brought about in a reaction catalyzed by acetaldehyde
dehydrogenase (E2 ), which produces acetic
acid from acetaldehyde: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
This sequence can be written in abstract notation as
|
|
|
|
|
|
|
|
|
|
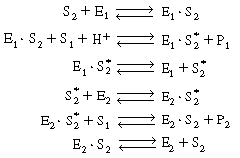
|
|
|
|
|
|
|
|
|
|
We could apply the PSSH to E1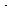 S2 , E1
S2 , E1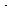 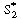 E2 , and E2
E2 , and E2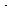 S and represent the total enzyme concentrations as
S and represent the total enzyme concentrations as |
|
|
|
|
|
|
|
|
|
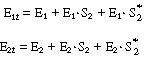
|
|
|
|
|
|
|
|
|
|
in deriving the rate law for this system. We shall not carry through
the necessary algebraic manipulation to obtain the rate law here, as all the principles
for determining the rate law have been presented, and there would be little more to
be accomplished by doing this.
The sections on enzymatic reactions were meant to serve as a brief,
yet somewhat encompassing discussion of enzyme kinetics. Further discussion
can be found in the Supplementary Reading for Chapter 9.
|
|
![]() -gluconolactone
(P):
-gluconolactone
(P):![]()
![]()
![]()
![]()
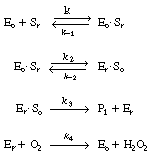
![]()
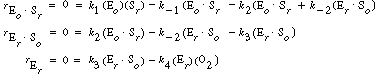
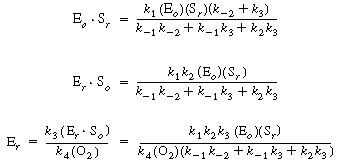
![]()
![]() Sr
) + (Er
Sr
) + (Er![]() So
) + (Er )
So
) + (Er )
![]()
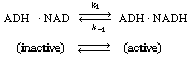
![]()
![]()
![]()
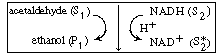
![]()
![]()
![]()
![]()
![]() NAD1
) complex could be converted by some means directly to the enzyme-cofactor
complex (ADH
NAD1
) complex could be converted by some means directly to the enzyme-cofactor
complex (ADH![]() NADH)
without having the enzyme ADH go through a series of reactions. This can
be achieved by the addition of a third substrate, S3
, (e.g., propanediol), which during reaction (to form DL-lactaldehyde)
will also regenerate the cofactor (NADH). The overall reaction sequence
for this case is
NADH)
without having the enzyme ADH go through a series of reactions. This can
be achieved by the addition of a third substrate, S3
, (e.g., propanediol), which during reaction (to form DL-lactaldehyde)
will also regenerate the cofactor (NADH). The overall reaction sequence
for this case is
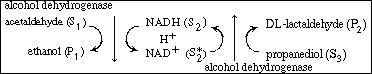
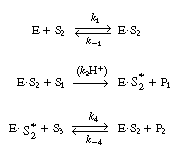
![]() NADH)
is believed to be rate limiting. This is con- firmed by the fact that
when ethanol was added to the system, the reaction rate increased 100-fold
by having the ethanol convert the (ADH
NADH)
is believed to be rate limiting. This is con- firmed by the fact that
when ethanol was added to the system, the reaction rate increased 100-fold
by having the ethanol convert the (ADH![]() NADH)
directly back to (ADH
NADH)
directly back to (ADH![]() NAD+
).
NAD+
).![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()