Ma316-001-F10 further explanation, §3.2
further explanation
existence and uniqueness
Consider two functions p(t) and q(t):
In[122]:=
![]()
Out[122]=

We know that the differential equation
y '' + p(t) y ' + q(t) y = 0,
with initial conditions
![]() ,
, ![]()
In[145]:=
![]()
Out[145]=

Has a unique solution:
In[125]:=
![]()
Out[125]=
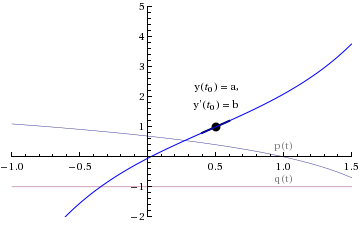
...as long as p(t) and q(t) are continuous
In[150]:=
![]()
![]()
Out[150]=

superposition of two (linearly independent) solutions can satisfy any initial condition
Now, suppose that we have two solutions, ![]() and
and ![]() , of
, of
y '' + p(t) y ' + q(t) y = 0
In[177]:=
![]()
Out[177]=

Then, if their Wronskian is non-zero at ![]() , given an initial condition there:
, given an initial condition there:
In[179]:=
![]()
Out[179]=

we can find a linear combination of ![]() and
and ![]() ,
, ![]() that solves the initial value problem
that solves the initial value problem
y '' + p(t) y ' + q(t) y = 0, ![]() ,
, ![]() :
:
In[202]:=
![]()
Out[202]=

superposition of two (linearly independent) solutions gives the general solution
Now suppose that we are given any solution φ(t) of the differential equation
y '' + p(t) y ' + q(t) y = 0.
We want to show that we can write φ(t) as a linear combination of ![]() and
and ![]() , that is, that we can find a
, that is, that we can find a ![]() and
and ![]() so that
so that
![]()
So, suppose that we have such a φ and that we know that at some point ![]() the Wronskian of
the Wronskian of ![]() and
and ![]() is non-zero.
is non-zero.
In[210]:=
![]()
Out[210]=

Then, at ![]() , we know that φ(t) satisfies the initial value problem
, we know that φ(t) satisfies the initial value problem
![]()
That is, a solution to the differential equation with the initial conditions:
In[249]:=
![]()
Out[249]=

That is, we're solving the differential equation with these initial conditions:
In[251]:=
![]()
Out[251]=

But, by the work in the previous section, we know that we can find a ![]() and a
and a ![]() such that
such that
![]()
satisfies the initial value problem
![]() .
.
Thus:
In[246]:=
![]()
Out[246]=

And the uniqueness theorem (the first section above) says that this solution is unique—that is, it must be the same function as the φ(t) that we started with:
In[248]:=
![]()
Out[248]=

Thus, because we started off with the assumption that φ(t) was any solution to the differential equation, we've shown that the linear combination
![]()
is the general solution to the differential equation!
Super cool!