|

|
Raman and Resonance Raman Spectroscopy on Metalloporphyrins
We have obtained the non-resonance Raman (NR Raman) spectra of [FeIII(TPP)Cl]
(TPP = tetraphenylporphyrin) including
polarized measurements for the first time as shown in Figure 1 and completely assigned these data using density functional (DFT) calculations.
In addition, resonance Raman (RR) data measured at variable wavelengths including new polarized data are presented and used to assign additional bands.
Finally, the IR spectrum of this compound has been assigned.
Group Theoretical Analysis
In order to assign the vibrational spectra of [Fe(TPP)Cl], an effective D4h symmetry was applied.
The analysis of the polarized data (see below) shows that this approach is justified even for five-coordinate compounds such as
[M(TPP)Cl] (M = Fe, Mn, Co). D4h symmetry is obtained for a planar porphyrin core with the metal being
located in the plane and no axial ligand present. The phenyl rings of TPP are exactly perpendicular to the porphyrin plane.
In this D4h model system [M(TPP)] (idealized metalloporphyrin), the planar porphyrin core has 71
in-plane modes [1]:
Γin plane = 9 A1g(R) + 8 A2g(RR) + 9 B1g(R) + 9 B2g(R) + 18 Eu(IR)
In the NR Raman spectrum, 27 in-plane vibrations are therefore expected, 9 of them polarized (A1g) and 18 depolarized
(B1g and B2g). The infrared spectrum shows a maximum of 18 modes with Eu symmetry. In addition,
the porphyrin core of the D4h model system has 34 out-of-plane vibrations [1]:
Γout of plane = 3 A1u + 6 A2u(IR) + 4 B2u + 5 B1u + 8 Eg(R)
The 8 Eg modes are Raman active and the 6 A2u modes are infrared active. Therefore, based on purely statistical consideration, much more in-plane
than out-of-plane modes can be expected in the NR Raman and IR spectra of metalloporphyrins.
Besides the porphyrin core modes, a large number of phenyl vibrations are also present in TPP complexes. Different approaches are possible for the classification of these
vibrations. In order to give an intuitive assignment of the phenyl modes of TPP, we use bromobenzene as a model.
The TPP ligand itself has four phenyl groups, which are bound to the meso carbon atoms of the porphyrin core. Hence, for every local phenyl
coordinate there are four symmetry-adapted combinations in TPP. Since the interactions of the local vibrations of different phenyl rings are small,
the obtained splittings between the resulting four combinations are also small (usually 5-10 cm-1). Hence, the four resulting symmetry
adapted linear combinations are also designated as a 'symmetry block', since they are close in energy. Since there are four different irreducible
representations in C2v (the point group of bromobenzene), four different symmetry blocks exist:
out-of-plane B1 leads to: B1g(R) + A2g(RR) + Eu(IR)
out-of-plane A2 leads to: A1u + B2u(RR) + Eg(R)
in-plane B2 leads to: B1u + A2u(IR) + Eg(R)
in-plane A1 leads to: A1g(R) + B2g(R) + Eu(IR)
In order to classify the different porphyrin core and phenyl modes in D4h symmetry, we used the idealized model [Zn(TPP)] and
calculated the vibrations of this model in D4h symmetry. [Zn(TPP)] has 169 normal modes (56 of them are degenerate),
where 44 % are Raman and 27 % are IR active.
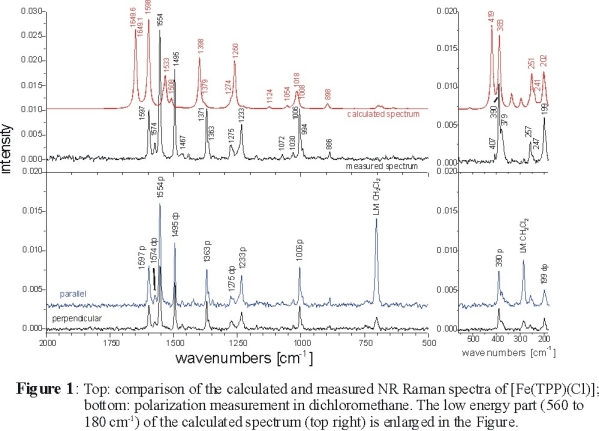
The experimental and calculated NR Raman spectra of [Fe(TPP)Cl] are shown in the top panel of Figure 1. Corresponding polarized data are
also included in the lower panel. The calculated spectrum is in general shifted to somewhat higher energy (the average deviation in vibrational energies
is about 2-3 %) compared to experiment. Besides the good agreement in vibrational frequencies, very good agreement with experiment is obtained for the
calculated NR Raman intensities. This allows for a detailed assignment of the data. Importantly, additional information to support the Raman assignments
is available from polarization measurements. The depolarization ratio ρ is defined as:
ρ = Iperpendicular / Iparallel
In D4h symmetry, one obtains [1]:
(a) 0 < ρ < 0.75: polarized bands (p) (A1g symmetry)
(b) ρ = 0.75: depolarized bands (dp) (B1g and B2g symmetry)
(c) ρ > 0.75: anomalous polarized bands (ap) (A2g symmetry; only RR active)
Hence, the polarized measurements allow for a determination of the symmetry of a mode. The complete assignments obtained this way are collected in
Table 3 in the reference given below.
Resonance Raman enhancement
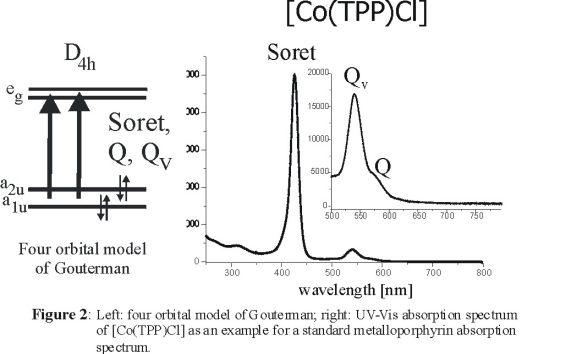
The electronic spectra of metalloporphyrins have been explained based on the four orbital model of Gouterman shown in Figure 2, left [2].
They are dominated by the two p to p* transitions from the a1u and a2u
HOMOs to the eg LUMO of the porphyrin dianion. Both resulting excited states have Eu symmetry and show strong configuration interaction
(CI). This leads to two well separated bands in the absorption spectra, the intense Soret band (where the individual transition moments are additive) and the
weak Q band (where they nearly cancel). In addition, a third band is observed on the higher energy side of Q. This band, Qv, is a result of
vibronic mixing between the Soret and the Q band. Since both excited states are of Eu symmetry, vibronic mixing is enabled by vibrations of
A2g, B1g and B2g symmetry. For the resonance Raman spectra of metalloporphyrins, A-, B- and C-term enhancement mechanisms
are important [3]. A-term enhancement is caused by a displacement of the excited state relative to the ground state and is in general only relevant for
totally symmetric (A1g) modes. Since A-term intensity is proportional to the square of the electric dipole transition moment of the excited
electronic state, this mechanism is dominant in the region of the Soret transition. B-term enhancement is caused by vibronic coupling between the excited
state |e> and another excited state |s>, which leads to resonance enhancement of the vibrations which are effective in coupling these states.
Hence, this mechanism applies to the Q band, where vibrations of A2g, B1g, and B2g symmetry are enhanced. Additional
A-term enhancement of A1g modes in the Q region is also expected. Importantly, resonance enhancement of non-totally symmetric modes is
therefore indicative for the presence of vibronic bands in the absorption spectra. However, B1g and B2g enhancement could
theoretically also be induced by a Jahn-Teller distortion of the excited states with Eu symmetry [4]. Hence, enhancement of A2g modes
is most diagnostic for the presence of vibronic coupling. A2g modes are easily identified in the Raman spectra due to their anomalous
polarization (ap; r > 3/4), which relates to the scattering tensor being antisymmetric [5]. Finally, C-Term enhancement is
observed upon excitation into a vibronic side band of a forbidden or weakly allowed 0-0 electronic transition which leads to enhancement of overtones
and combination modes [3]. This applies to the Qv region of the absorption spectra. These different types of resonance enhancement are indeed
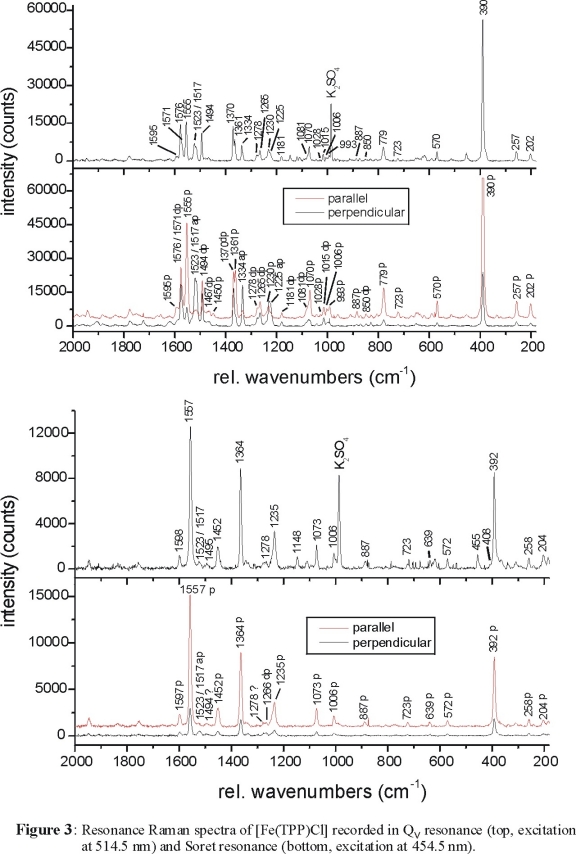
observed for [Fe(TPP)Cl] as shown in Figure 3, top (recorded in Qv resonance with excitation at 514.5 nm). In comparison,
Figure 3, bottom shows the spectrum obtained in Soret resonance (excitation at 454.5 nm). The RR data in the Soret region are dominated by polarized
(A1g) bands, which can therefore easily be identified from the Soret spectrum. The Q and Qv spectra contain depolarized,
polarized and anomalous polarized bands. The presence of A2g vibrations in the Q and Qv spectra nicely confirms the presence of
vibronic coupling as already discussed. The Qv RR spectra also show overtones and combination bands above 1600 cm-1 corresponding
to C-Term enhancement, which confirms that Qv is the vibronic side band of Q.
Effect of Symmetry Lowering
There are three major effects resulting from the symmetry lowering from idealized D4h to the actual symmetry of
[Fe(TPP)Cl]. Due to the fact that the phenyl rings are no longer perpendicular to the porphyrin core, coupling between the core and the phenyl
vibrations becomes stronger. The second effect is that modes with different symmetries in D4h appear mixed in [Fe(TPP)Cl].
Several examples are observed in the NR Raman and IR spectra, where even (g) and odd (u) vibrations are combined. This applies for example to the NR Raman
bands at 247 and 257 cm-1 and IR bands at 390, 727 and 1574 cm-1 (see reference given below). Importantly though, all these
'symmetry breaking' modes only obtain very small intensities due to this 'intensity stealing' mechanism. This, together with the observation of
polarized, depolarized and anomalous polarized bands clearly shows that the [Fe(TPP)]+ core still behaves as if it has
D4h symmetry. The third effect of symmetry lowering beyond C4v is that degenerate Eu vibrations appear split
in the IR spectra. However, the observed splittings are very small (about 5 cm-1). Hence, this again indicates that an effective
D4h symmetry is present even in the five-coordinate complex [Fe(TPP)Cl].
Reference:
F. Paulat, V. K. K. Praneeth, C. Näther, N. Lehnert
"Quantum Chemistry-Based Analysis of the Vibrational Spectra of Five-Coordinate Metalloporphyrins [M(TPP)Cl]"
Inorg. Chem. 2006, 45, 2835-2856
M. W. Wolf, K. Rizzolo, S. J. Eliott, N. Lehnert
"Resonance Raman, Electron Paramagnetic resonance, and Magnetic Circular Dichroism Spectroscopic Investigation of Diheme
Cytochrome c Peroxidases from Nitrosomonas europaea and Shewanella oneidensis"
Biochemistry 2018, 57, 6416-6433
Literature:
[1] Spiro, T. G. in Iron porphyrins; Lever, A. B. P.; Gray, H. B., Eds.; Addison-Wesley: Massachusetts, 1983, part 2, pp 89-159.
[2] Gouterman, M. in The Porphyrins; Dolphin, D., Ed.; Academic: New York, 1979, Vol. III, Part A, pp 1-156.
[3] Czernuszewicz, R. S.; Spiro, T. G. in Inorganic electronic structure and spectroscopy; Solomon, E. I., Lever, A. B. P., Eds.;
John Wiley & Sons: New York, 1999, Vol. I, pp 353-441.
[4] Egawa, T.; Suzuki, N.; Dokoh, T.; Higuchi, T.; Shimada, H.; Kitagawa, T.; Ishimura, Y. J. Phys. Chem. A 2004, 108, 568-577.
[5] Spiro, T. G.; Strekas, T. C. Proc. Nat. Acad. Sci. USA 1972, 69, 2622-2626.
|




