By Shiming Duan,  Last Update: 8/11/2010 3:03 PM

 

 

II.            Solution of Systems of DDEs via the Matrix Lambert W Function

 

Although the major challenge in studying DDEs comes from its infinite spectrum of frequencies, an exact determination of the spectrum is very hard but valuable. In Chapter 2 of the book, analytical solutions for scalar DDEs as well as general DDEs are obtained using the Lambert W function. Here, we will focus on showing the procedures for finding the solutions for such DDEs.

 

2.1 Scalar Case

 

Consider the first-order scalar DDEs:

where , ,  are all scalar constants,  is the time variable,  is initial state at and ,  are scalar functions. Note that a discontinuity may exist at t = 0 if . The solution of scalar DDEs can be written in terms of the Lambert function, ,

, 

where  ,  and

 

 

Example 2.1: Consider the hydraulic system in Example 1.1. Let A=10m2,  =1000kgm-3, g=10ms-2, R=10m-1/2 kg-1/2, =1s, K=-1000. Therefore, the closed-loop system is

We want to derive the analytical solution for this free response of this system with initial state x(0)=10, . Using the method for a scalar DDE, we can calculate Sk,, for each branch.

For example, when k=0,

In Matlab, one can use the following codes to calculating these two coefficients.

 

S_0 = lambertw(0,-0.1*exp(0.1))

CI_0 = 10/(1-0.1*exp(0.2263))

 

The results for some other branches are listed in the following table:

 

Branch, K

2

1

0

-1

-2

-3

Sk

-4.9861+13.7968i

-4.4439+7.3183i

-0.2253

-3.53722

-4.4439-7.3183i

-4.9861- 13.7968i

-0.1891-0.6715i

-0.5165-1.1304i

11.432

-4.1030

-0.5165+1.1304i

-0.1891+0.6715i

 

 

Thus, the free response of the system can be determined from the following equation:

and can be approximated by summing a finite number of branches. The figure 1.2 shows the convergence of the solution as the number of branches are increased.

 

2.2 Matrix Case

 

Consider the system of DDEs in matrix-vector form:

where  and are  coefficient matrices, are  coefficient matrices, is an  state vector, is an  input vector, is an  preshape function, t is time, and h  is a constant scalar time delay. The reponse of the free system can be obtained as:

where

and  is solved by the following condition

The coefficients  are determined from specified preshape function  and initial state  and can be calculated using either of two methods (Yi et al., 2006, 2007), as illustrated in the example below.

 

Procedure:

For each branch :

1.      Check the rank of  to decide on the form of the solution

a.       If Ad has a full rank, regular approach can be used (e.g., see Example 2.2)

b.      If Ad does not have a full rank, one must use hybrid branch approach (e.g., see Example 2.3). 

2.      Compute from the condition above using the fsolve function in Matlab

a.       Select a proper initial condition Q_initial (e.g., identity matrix or  may be good candidates for Q_initial)

b.      Define the equation  for the function fsolve(@F, Q_initial, options)

c.       Call the fsolve function and check if it returns a solution; If neccessary, set different Q_initial and redo Step 1

3.      Compute  from the matrix Lambert W function

4.      Compute  and  using either of two methods (Yi et al., 2006, 2007)

 

Example 2.2: Consider the following matrix DDE:

 

Determine the solution for the DDE with  and  .

 

Step 1.  Check the rank of. In this example,  has a full rank and regular procedure can be used.

Step 2.  Solve Qk  for each branch using the fsolve function. For example, when K=0, one need to solve for Q0  which satisfies

.

 The matlab code for this step is listed below

 

% Written by Sun Yi Sept. 30, 2009
% Dept. Mechanical Engineering, University of Michigan  
% Phone: (734) 763-2227
% Email: syjo@umich.edu                               
% Matrix Function: Compute Qk
 
global h k1 k2 A Ad I                  % Define variable for fsolve
 
k1 = 1;k2=k1;                          % Branch of the matrix Lambert W function
I     =  eye(2);                          % for identity matrix
h     =  1;                                  % time-delay
A     =  [-1 -3;2 -5]; Ad    =  [1.66 -0.697;0.93 -0.330]; % coefficient matrices of the system A=-Ad;B=-A
x0=I;                                             % initial condition for interation => identity matrix  
tol=1e-8;options = optimset('MaxFunEvals',1000,'TolFun',1e-8); % iteration options

        X   =  fsolve(@equations,x0,options)                          % iteration

 

 
function rtn=equations(x)
global h k1 k2 A Ad I
X     = [x(1) x(2) x(3) x(4)];
Q     =  [x(1) x(2);x(3) x(4)];D =  Ad*h*Q;
[v,d] =  eig(D);
W     =  v*[lambertw(k1,d(1,1)) 0;0 lambertw(k2,d(2,2))]*inv(v); % for matrix Lambert W function (Eq. (2.16)) in book
EX    =  expm(W+A*h);
Left  =  (W*EX);                                              % the left side of Eq. (2.19) in book
Right =  Ad*h;                                                  % the right side of Eq. (2.19) in book 
rtn   =  [Left(1,1)-Right(1,1)
          Left(1,2)-Right(1,2)    
          Left(2,1)-Right(2,1)
          Left(2,2)-Right(2,2)];                              % Eq. (2.19) in book 
 

 

Step 3. After Qk  is obtained, one should compute  using the equation 

Q   =  [X(1) X(2);X(3) X(4)]                                    % result for Qk
D     =  -A*T*Q;[v,d] =  eig(D);                                % To compute Sk    
W     =  v*[lambertw(k1,d(1,1)) 0;0 lambertw(k2,d(2,2))]*inv(v);
Sk     =  1/T*W-B                                               % result for Sk 

 

Step 4.  Compute  and . Here we apply the Laplace tranform based approach (Yi et al., 2006b) and use Eq. (2.58) and Eq. (2.60) from the book to evaluate the coefficients for each branch. For example, for k=0, we have

, ,  

Thus,

 ,

 

  

  

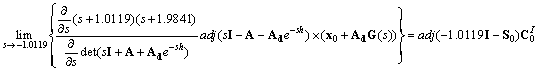
Note that the two equations associated with the same eigenvalue are linearly dependent. Thus, one must solve the four equations simultaneously to calculate . Here we combine the first equation from  and first equation from  and obtain .

Similarly, one can obtain  from Eq. (2.60) in the book

 

 

Again, we combine the first equation from  and first equation from  and obtain :

 

The matlab code for this step is listed below

 

    [V_Sk, D_Sk]=eig(Sk);                                                 eigenvalue of Sk

    eig_Sk = [D_Sk(1,1) D_Sk(2,2)];

    for jj=1:2

        s=eig_Sk(jj);

        %%%%%%%%%%%%%%%%%%second

        up=2*s-eig_Sk(1)-eig_Sk(2);                                               % Equations (2.58) and (2.60) in book 

        down=2*s+307/125*exp(-s)+133/100*s*exp(-s)+6-10041/50000*exp(-s)^2;

        Second=up/down;

        %%%%%%%%%%%%%%%%%%third

        Char=s*I-Ad*exp(-s*T)-A;

        Third=[Char(2,2) -Char(1,2);-Char(2,1) Char(1,1)];

        %%%%%%%%%%%%%%%%%%Fourth

        Fourth=[1;0]+Ad*[1/s-exp(-s*h)/s;0];                                  % Using Initial Conditions

        %%%%%%%%%%%%%%%%%%left

        Left(:,jj)=Second*Third*Fourth;

        Left1(:,:,jj)=Second*Third;

        %%%%%%%%%%%%%%%%%%first

        First(:,:,jj)=s*I+[-Sk(2,2) Sk(1,2);Sk(2,1) -Sk(1,1)];

    end

    %%%%%%%%%%%%%%%%%% Ck

    for ii=1:1

        Rig=[First(ii,1,1) First(ii,2,1);First(ii,1,2) First(ii,2,2)];

        C_I = inv(Rig)*[Left(ii,1);Left(ii,2)];

    end

    %%%%%%%%%%%%%%%%%% Ck prime

    Rig1=[First(1,1,1) First(1,2,1);First(1,1,2) First(1,2,2)];

    Cprime = inv(Rig1)*[Left1(1,1,1) Left1(1,2,1);Left1(1,1,2) Left1(1,2,2)];

 

 

The results for some other branches are listed in the following table:

 

Similar to the scalar case, the response of the system of matrix DDEs can be determined from the following equation:

and can be approximated by summing a finite number of branches. The solution obtained using the Lambert W function approach for 11 branches is compared in Figure 2.1 with the simulation results using the Matlab dde23 function.

 

Fig. 2.1 Comparison between the solution obtained using the Lambert W function method with 11 branches (solid) to the results using the Matlab dde23 function (dash)

(Fig. 2.5 in book)