By Shiming Duan, Last Update: 8/11/2010 3:03 PM
III. Stability of Systems of DDEs via the Lambert W Function
One advantage for the Lambert W function based approach is that it enables us to locate the poles of the principal branch and use the result to determine the stability of a system of DDEs. For example, we can use this method to design the control of DDEs with guarrenteed closed-loop stability and performance. Here we summarize the results of the stability analysis of DDEs using the Lambert W function.
Scalar Case
It has been proven in (H. Shinozaki and T. Mori, 2006)
that, for the scalar DDEs, the rightmost pole in the s-plane is determined by
the principal branch (![]() ) of
) of ![]() . Thus,
. Thus,

One can use only the principal branch to determine the stability of scalar DDEs.
Matrix Case
The proof for the scalar case can
readily be extended to the matrix case when ![]() and
and![]() are simultaneously triangularizable (Radjavi and
Rosenthal, 2000). No such proof
is currently available for the general case of matrix DDEs. However, in all the
examples considered in the literature, it has been observed that the rightmost
eigenvalue is obtained using the first m branches, where m is the
nullity of
are simultaneously triangularizable (Radjavi and
Rosenthal, 2000). No such proof
is currently available for the general case of matrix DDEs. However, in all the
examples considered in the literature, it has been observed that the rightmost
eigenvalue is obtained using the first m branches, where m is the
nullity of ![]() . We state this here as a generalization
of the conjecture in the book (see section 3.3.1 in the book):
. We state this here as a generalization
of the conjecture in the book (see section 3.3.1 in the book):
![]()
where ![]() .
.
When ![]() has no repeated zero
eigenvalues:
has no repeated zero
eigenvalues:
![]()
Thus, if ![]() has no
repeated zero eigenvalues, or
has no
repeated zero eigenvalues, or ![]() has full
rank, one can use only the principal branch to determine the stability of
matrix DDEs. Otherwise, all the first m branches must be examined to yield
a conclusion.
has full
rank, one can use only the principal branch to determine the stability of
matrix DDEs. Otherwise, all the first m branches must be examined to yield
a conclusion.
Example 3.1: Consider the pendulum system in example 1.2. Let l=2m, m=1kg, g=10ms-2 , ![]() and
and ![]() =1s.
The control is a velocity feedback control
=1s.
The control is a velocity feedback control  .
The physical meaning of the control is to add delayed damping to stabilize the
system and the objective is to determine
.
The physical meaning of the control is to add delayed damping to stabilize the
system and the objective is to determine
the proper coefficient c for the controller so that the closed-loop system described in the following equation is stable. Further, we are interested in the free response of the closed-loop system
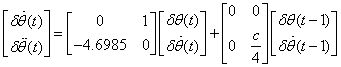
under a certain initial
condition ![]() .
.
Step 1. First,
check the rank of![]() . In this example,
. In this example, ![]() has a rank of one if
has a rank of one if ![]() since
since ![]() . Thus, we can use only the
principal branch to check the stability of the DDE. If
. Thus, we can use only the
principal branch to check the stability of the DDE. If ![]() , the DDE becomes an ODE and one
can verify that the system is not asymptotically stable since
, the DDE becomes an ODE and one
can verify that the system is not asymptotically stable since ![]() . Since one of the eigenvalues of
. Since one of the eigenvalues of ![]() is
zero, the regular approach (see Ex. 2.2) cannot be used because
is
zero, the regular approach (see Ex. 2.2) cannot be used because ![]() . Thus, one must apply the hybrid
branch approach to solve the problem.
. Thus, one must apply the hybrid
branch approach to solve the problem.
Step 2. Solve Q0,0 for the principal branch using the fsolve function.
Let  and
we have
and
we have 
One
can verify that the Jordan canonical form of ![]() is
is

The matrix Lambert W function with hybrid branches are defined as
 .
.
Thus, Q0,0 satisfies
![]()
Step 3.
After ![]() is obtained, we can compute
is obtained, we can compute ![]() from the equation
from the equation ![]() . Based on the conjecture, we can determine the
stability of the system based on
. Based on the conjecture, we can determine the
stability of the system based on ![]() . One can verify, using either
the Lambert W function approach or Matlab dde23 function, that the
closed-loop system is stable when
. One can verify, using either
the Lambert W function approach or Matlab dde23 function, that the
closed-loop system is stable when ![]() . Here we pick
. Here we pick ![]() and obtain
and obtain ![]() . The table below lists the results for different values of c.
. The table below lists the results for different values of c.
|
C |
c = -2 |
c = 2 |
c = 4 |
c = 6 |
c = 8 |
|
Q0,0 |
|
|
|
|
|
|
S0,0 |
|
|
|
|
|
|
|
|
|
|
|
|
Step 4. After c is selected, we need to obtain the solution of the closed-loop DDE. For branches other than the principal branch, we must use the matrix Lambert W function with hybrid branches, which is defined as
 .
.
By setting k2=0
and letting k1 vary from ![]() to
to ![]() ,
we can solve Eq. (2.15) in book to obtain
,
we can solve Eq. (2.15) in book to obtain ![]() .
After
.
After ![]() is obtained, we can compute
is obtained, we can compute ![]() from the equation
from the equation ![]() . The following table shows the results for part of
the branches.
. The following table shows the results for part of
the branches.
|
|
|
Eigenvalues of |
|
k1=0 & k2=0 |
|
|
|
k1=-1 & k2=0 |
|
|
|
k1=1 & k2=0 |
|
|
|
k1=-2 & k2=0 |
|
|
|
k1=2 & k2=0 |
|
|
Remark:
When Ad
does not have full rank and the hybrid branch approach is applied, it is
possible to find more than one solution for each ![]() , the non-principal branches. One may find different
, the non-principal branches. One may find different ![]() for a certain branch by using different initial conditions to
initialize the fsolve function to solve the equation
for a certain branch by using different initial conditions to
initialize the fsolve function to solve the equation
![]()
In this example, k2 =
0 and k1 =![]() ,...,-1, 0, 1, ...,
,...,-1, 0, 1, ...,![]() . From the results, we observe that
the eigenvalues in the principal branch are repeated in the non-principal
branches, which arises due to by fixing k2 =
0 when calculating the hybrid matrix Lambert W function. We also note that some
eigenvalues from the non-principal branches appear in other non-principal branches,
which also makes this case very special. Because of these special features, for
the rest of the steps, it is more convenient to find the solution using the
following procedure instead of the general one introduced in Ex. 2.2.
. From the results, we observe that
the eigenvalues in the principal branch are repeated in the non-principal
branches, which arises due to by fixing k2 =
0 when calculating the hybrid matrix Lambert W function. We also note that some
eigenvalues from the non-principal branches appear in other non-principal branches,
which also makes this case very special. Because of these special features, for
the rest of the steps, it is more convenient to find the solution using the
following procedure instead of the general one introduced in Ex. 2.2.
For the hybrid branch case (rank(Ad)<n), one should
* Find the set of distinct
eigenvalues ![]() , j =
, j =![]() ,...,-1, 0, 1, ...,
,...,-1, 0, 1, ...,![]() ,
from the results for
,
from the results for ![]() . Note here
. Note here ![]() are scalars instead of
matrices. In this example, the set of distinct eigenvalues is
are scalars instead of
matrices. In this example, the set of distinct eigenvalues is ![]() .
.
* Use approaches similar to partial
fraction expansion to find coefficients ![]() for each
for each ![]() (see Step 5 below)
(see Step 5 below)
* The solution of the free response can then be obtained as
![]() ,
where
,
where ![]() and
and ![]()
Note here ![]() and
and ![]() are
vectors with same dimension and
are
vectors with same dimension and ![]() are
scalar functions of time. The multiplicity of
are
scalar functions of time. The multiplicity of ![]() can
be determined by evaluating the limit
can
be determined by evaluating the limit
![]()
The smallest
natural number q satisfying the above equation is the multiplicity of ![]()
Step
5. To compute ![]() , one should solve the partial fraction expansion for this infinite
series. When the multiplicity of
, one should solve the partial fraction expansion for this infinite
series. When the multiplicity of ![]() , the solution can be formulated as
, the solution can be formulated as
![]()
and the ![]() can be determined as
can be determined as
![]()
For the case
when the multiplicity of ![]() , one can take
the derivative of the numerator and denominator first before evaluating the
limit (similar to the PFE for a
ratio of two polynomials). For example, when
, one can take
the derivative of the numerator and denominator first before evaluating the
limit (similar to the PFE for a
ratio of two polynomials). For example, when ![]() has
multiplicity of 2 while the other distinct eigenvalues have multiplicity of 1:
has
multiplicity of 2 while the other distinct eigenvalues have multiplicity of 1:
![]()
Then

The table
below lists the results for ![]() under
the initial condition
under
the initial condition ![]()
|
Index j |
Eigenvalue |
Multiplicity of |
Coefficient |
|
1 |
|
1 |
|
|
2 |
|
1 |
|
|
3 |
|
1 |
|
|
4 |
|
1 |
|
|
5 |
|
1 |
|
|
6 |
|
1 |
|
|
7 |
|
1 |
|
|
8 |
|
1 |
|
Thus, the free response of the matrix DDE system in this example can be determined as
![]()
and can be approximated by summing a finite number of branches. The solution obtained using the Lambert W function approach for the first 8 distinct eigenvalues is compared with the simulation results using the Matlab dde23 function in Fig.3.1.

Fig. 3.1 Comparison between the solution obtained using the Lambert W function method for the first 8 distinct eigenvalues (solid) to the results from the Matlab dde23 function (dash) for Example 3.1