By Shiming Duan,  Last Update: 8/13/2010 5:01 PM

 

IV.         Controllability and Observability of Systems of DDEs

In Chapter 2 and Chapter 3, analytical solutions for systems of DDEs have been derived. These results are extended in this chapter to investigate the point-wise controllability and observability and their Gramians for linear time-delay systems.

Again, consider the system of DDEs in matrix-vector form:

where  and are  coefficient matrices, are  coefficient matrices, is an  state vector, is an  input vector, is an  preshape function, t is time, and h  is a constant scalar time delay. The coefficient matrix C is  and y(t) is a  measured output vector.

 

Point-wise Controllability

The system of DDEs is point-wise controllable if, for any given initial conditions g(t) and x0, there exists a time t1, 0 < t1 < , and an admissible (i.e., measurable and bounded on a finite time interval) control segment u(t) for  such that x(t1; g, x0, u(t)) = 0 (Weiss,1967).

 

The following three sufficient and necessary conditions for point-wise controllability of systems of DDEs are equivalent.

The system of DDEs is point-wise controllable if and only if :

 

*  

 

where  is the controllability Gramian of the system of DDEs

 

*  All rows of

are linearly independent on .

 

 

*  All rows of

        

are linearly independent over the field of complex number except at the roots of the characteristic equations of system of DDEs.

 

 

 

Point-wise Observability

The system of DDEs is point-wise observable in [0, t1] if the initial point x0 can be uniquely determined from the knowledge of u(t), g(t), and y(t) (Delfour and Mitter, 1972).

 

The following three sufficient and necessary conditions for point-wise observability of systems of DDEs are equivalent.

The system of DDEs is point-wise observable if and only if:

*  

 

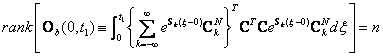
where  is the observability Gramian of the system of DDEs

 

*   All rows of

are linearly independent on .

 

 

*   All rows of

are linearly independent over the field of complex number except at the roots of the characteristic equations of system of DDEs.

 

 

 

Example 4.1: Consider the following second-order time-delay systems:

where x1, x2 are the two states of the system, h is the time delay, u is the input and c1, c2 are the parameters for matrix Ad. In this example, we will investigate the controllability of the system for different values of c1,and c2:

Case 1: c1= c2 =0

Case 2: c1=0.1, c2 =0

Case 3: c1=0, c2 =0.1

 

Case 1: when c1= c2 =0, the system of DDEs will resort to a system of ODEs:

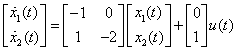
One can verify that the system is uncontrollable by checking the rank of the controllability matrix:

Thus, the system of ODEs is not controllable.

 

 

Case 2: When c1=0.1, c2 =0, the system becomes

One can calculate the controllability Gramian of the system of DDEs using the approach introduced in this chapter. First, we can use similar approach introduced in Ex. 3.1 to obtain  and  for the system of DDEs.

 

 

Index j

Eigenvalue

Coefficient

1

-0.7815

2

-2

3

-3.9173+4.0932i

4

-3.9173-4.0932i

5

-4.7267+10.6592i

6

-4.7267-10.6592i

7

-5.1671+17.0389i

8

-5.1671-17.0389i

9

-5.4721+23.3729i

10

-5.4721-23.3729i

 

 

 

 

Second, we evaluate controllability Gramian of the system of DDEs

 

 

Here, we pick t1=4. Please note that the result of controllability does not depend on the selection of t1 since the sytem is linear. From Fig.4.1, we can see that controllability Gramian does not have full rank even more branches are considered. Thus, the system is not point-wise controllable by checking the rank of the controllability Gramian.

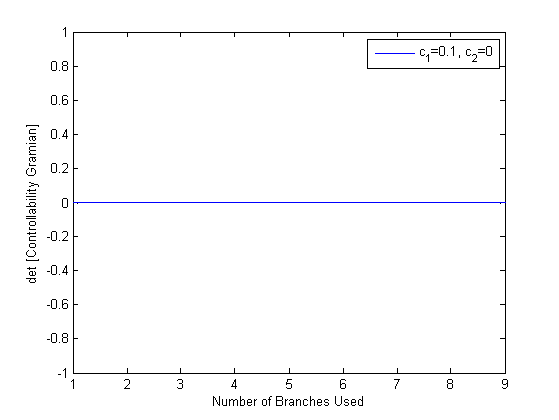
Fig. 4.1 Determinant of controllability Gramian for Case 2 in Ex.4.1.

The value of determinant is a constant zero when more branches are used.

 

 

Case 3: When c1=0, c2 =0.1, again, one can use Gramian to check the controllability.

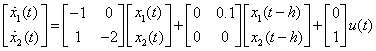
Again, we obtain  and  for the system of DDEs first.

 

 

Index j

Eigenvalue

Coefficient

1

-0.8108

2

-3.0086

3

-4.4064+1.0364i

4

-4.4064-1.0364i

5

-6.8827+8.2735i

6

-6.8827-8.2735i

7

-7.8740+14.9002i

8

-7.8740-14.9002i

9

-8.5284+21.3555i

10

-8.5284-21.3555i

 

 

Here, we pick t1=4 and calculate the obser Gramian.

 

 In Fig.4.2, we can see that the determinant of the controllability Gramian converges to non-zero values. Thus, the controllability Gramian has full rank and the system is point-wise controllable.

Fig. 4.2 Determinant of controllability Gramian for Case 3 in Ex.4.1.

The value of determinant converges to a non-zero value as more branches are considered.

 

 

 

Example 4.2: Consider the closed-loop pendulum control system discussed in Ex.3.1. It is assumed that only the angular velocity of the pendulum is measured and the control is a velocity feedback control . In this example, if only the velocity is measured, we want to know whether we can

 

reconstruct the other state, the angular position, from the measurements. In other words, we want to check whether the closed-loop time delay system is point-wise observerable.

The procedure here is quite similar to the procedure introduced in Ex.4.1. First, we obtain  and  for the system of DDEs.

 

 

Index j

Eigenvalue

Multiplicity of

Coefficient

1

1

2

1

3

1

4

1

5

1

6

1

7

1

8

1

 

Then, we pick t1=4 and calculate the observability Gramian.

 

In Fig.4.3, we can see that the determinant of the observability Gramian converges to non-zero values. Thus, the observability Gramian has full rank and the system is point-wise observable.

 

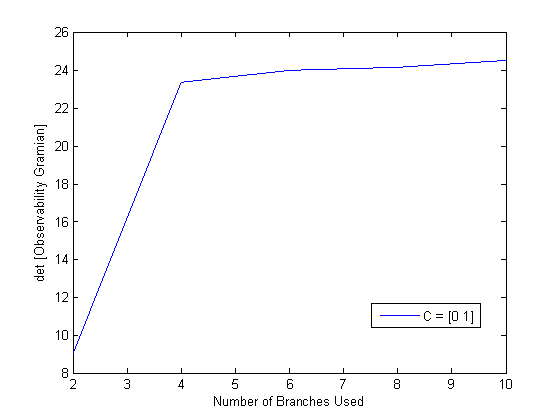
Fig. 4.3 Determinant of observability Gramian of the system in Ex.4.2.

The value of determinant converges to a non-zero value as more branches are considered.