By Shiming Duan, Last Update: 8/13/2010 5:09 PM
VI. Robust Control and Time-Domain Specification via Eigenvalue Assignment
In Chapter 5, the method for eigenvalue assignment via the Lambert W function was introduced. In practice, systems are usually subject to various kinds of uncertainties, which may come from estimation errors, approximation errors or modeling errors. To ensure the performance of the design for such perturbed systems, it is important to consider the effects of these uncertainties. In this chapter, a new approach based on the Lambert W function is proposed to solve the robust control problem for systems of DDEs. Furthermore, a method based on the analysis of rightmost eigenvalues is proposed to help the design of feedback control systems achieve desired time-domain specification.
Stability Radius
To calculate the stability radius for a perturbed time delay system
![]()
one can follow the following procedure:
Step 1: Calculate 
Step 2: Calculate
 where
where ![]() and
and ![]() are the largest and smallest
singular values of
are the largest and smallest
singular values of ![]()
Step 3: Find the maximum value of  over the interval
over the interval ![]() , where
, where 
Since ![]() , the maximum
value find in Step 3 will be the supremum value of
, the maximum
value find in Step 3 will be the supremum value of

which gives the stability radius of the system with uncertainty.
Robust Feedback Control Design
Step 1: Compute the stability radius, ![]() , of
the given system , where
, of
the given system , where ![]() denotes
the largest singular value of
denotes
the largest singular value of ![]()
Step 2: Apply the method introduced in Chapter 5 to select feedback gains
Step 3: Compute a theoretical stability radius, r2, of the closed-loop system using the procedure introduced above
Step 4: If r1 > r2, then system may be destabilized by the uncertainty; go back to step 2 and select a more conservative gain (the gain that moves the rightmost poles farther to the left in the s-plane)
Design Based on Time-Domain Specifications
Using the Lambert W function approach, one can not only assign the real parts of the rightmost eigenvalues, but also their imaginary parts. It is not feasible to assign the entire eigenspectrum by using a finite number of control parameters. However, since rightmost poles usually dominate the transient responses of the systems of DDEs, design based on rightmost eigenvalues will often provide a good approximation.
For ideal second-order system of ODEs, the time-domain specifications can be calculated as
![]()
For systems of DDEs, although there are infinite number of eigenvalues, approximating these specifications from rightmost eigenvalues still provides useful information for design.
Example 6.1 Nonlinear Hydraulic System (Robust Feedback Control)
Consider the hydraulic water tank system with the nonlinear model
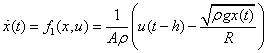
and the parameters have the same values as in Ex. 5.1. In this example, a feedback control for this nonlinear system will be designed to keep the level of water at x0=0.5m. Compared to the linear model used in Ex. 5.1, this nonlinear model has both nonlinear terms and delay terms. Here we will demonstrate how to apply the Lambert W function approach to solve a robust feedback control problem.
First, note that ![]() and linearize
the system about the equilibrium point (x0, u0):
and linearize
the system about the equilibrium point (x0, u0):

where ![]() and
and ![]() represents the approximation
error from the Taylor expansion. Assume that the depth of the tank is 1m
and the level of the water surface is measurable. Therefore, with
represents the approximation
error from the Taylor expansion. Assume that the depth of the tank is 1m
and the level of the water surface is measurable. Therefore, with ![]() , the closed-loop system becomes
, the closed-loop system becomes

The approximation error for ![]() (
(![]() ) is shown in Fig.6.1. Thus, one can
obtain the bounds
) is shown in Fig.6.1. Thus, one can
obtain the bounds ![]() for the figure.
for the figure.

Fig.6.1 Uncertainty raised due to approximation error
First, one can easily obtain ![]() .
Then, choose the gain K to place the rightmost eigenvalue. A list of
gains and corresponding rightmost eigenvalues is listed in the following table.
In Fig. 6.2, it can be seen that the stability radius increases as the
eigenvalue moves left. Since
.
Then, choose the gain K to place the rightmost eigenvalue. A list of
gains and corresponding rightmost eigenvalues is listed in the following table.
In Fig. 6.2, it can be seen that the stability radius increases as the
eigenvalue moves left. Since ![]() ,
we can place the rightmost eigenvalue at -2 with a stability radius of
,
we can place the rightmost eigenvalue at -2 with a stability radius of ![]() such
that the system will remain stable despite the uncertainty.
such
that the system will remain stable despite the uncertainty.
Table 6.1 The gains K corresponding to each rightmost eigenvalues
|
Rightmost Eigenvalues |
−0.0009 |
−0.0011 |
−0.0013 |
−0.0015 |
−0.0017 |
−0.00019 |
|
K |
|
|
|
|
|
|

Fig.6.2 The rightmost eigenvalues vs. the stability radius of the system in Ex.6.1
Example 6.2 Pendulum System (Design based on Time-Domain Specification)
Consider again the eigenvalue assignment problem for the pendulum system in Ex. 5.2 .

where ![]() and
and
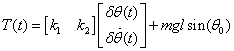
In Ex. 5.2, we designed a full state feedback control and assigned the
rightmost poles to be ![]() . The selection of the
rightmost eigenvalues is surely not unique. In this example, we will find the
relationship between the performance of the system and the location of rightmost
eigenvalues.
. The selection of the
rightmost eigenvalues is surely not unique. In this example, we will find the
relationship between the performance of the system and the location of rightmost
eigenvalues.
Follow the same procedure introduced as in Ex.5.2 to place the right
poles at ![]() and
and ![]() with different feedback
gains. As shown in the Table 6.2, although the three pairs of poles considered
have the same real parts, the transient responses can be quite different
depending on the selection of the imaginary parts. Therefore, one can assign
the rightmost eigenvalues based on the estimated performance first and validate
the actual performance by simulation afterwards (see Fig.6.3). Although
analysis based on rightmost eigenvalues only provides an approximation, the
method gives useful guidelines for design.
with different feedback
gains. As shown in the Table 6.2, although the three pairs of poles considered
have the same real parts, the transient responses can be quite different
depending on the selection of the imaginary parts. Therefore, one can assign
the rightmost eigenvalues based on the estimated performance first and validate
the actual performance by simulation afterwards (see Fig.6.3). Although
analysis based on rightmost eigenvalues only provides an approximation, the
method gives useful guidelines for design.
Table 6.2 The rightmost eigenvalues with corresponding time-domain specifications
|
Rightmost Eigenvalues |
|
|
|
|
K |
|
|
|
|
|
1.5 |
2 |
2.5 |
|
|
1.80 |
2.24 |
2.69 |
|
|
0.555 |
0.447 |
0.371 |
|
|
0.999 |
0.805 |
0.669 |
|
|
4.6 |
4.6 |
4.6 |
|
|
2.094 |
1.571 |
1.257 |
|
|
12 |
21 |
28 |

Fig.6.3 Responses of the systems with feedback control corresponding to the rightmost eigenvalues in Table 6.2