By Shiming Duan,  Last Update: 8/15/2010 2:04 PM

VIII. Eigenvalue and Sensitivity Analysis for Systems of DDEs

In this chapter, we will focus on the eigenvalues and sensitivity analysis for systems of DDEs using the Lambert W function approach. Eigenvalue analysis can help to understand the relationship between rightmost eigenvalues and system parameters. Further, the result is extended to sensitivity analysis, which further quantifies the influence of the parameters on the dynamics of systems. In the rest of this chapter, we will perform these analyses on the 1^st order water tank system and the 2^nd order pendulum system for an illustration.

Example 8.1: Water Tank System

Consider the linear model of the hydraulic system in Example 1.1.

We will explore the relationship between the rightmost eigenvalues of the system and the cross-sectional area  as well as the hydrodynamic resistance.  The nominal values of the parameters are the same as in Ex. 5.1 (A=10m², =1000kgm^-3, g=10ms^-2 , h =1s, R=10m^-1/2 kg^-1/2, K=−1000).

Rightmost Eigenvalue Analysis

First, calculate the rightmost eigenvalues of the systems with all nominal parameter values except R=(0.5:0.1:1.5)R_nom, where R_nom  is the nominal hydrodynamic resistance. The result for the rightmost eigenvalues is shown in Fig.8.1. As illustrated in the figure, when R increases, the rightmost eigevalue of the system moves further to the right of the s-plane, indicating an decreased stability of the system.

Similar procedure is used to analyze the parameter A. Calculate the rightmost eigenvalues of the systems with all nominal parameter values except A=(0.5:0.1:1.5)A_nom, where A_nom  is the nominal cross-sectional area.  In Fig.8.2, it is observed that the rightmost eigevalue of the system moves further to the right of the s-plane as A is increased.

Fig.8.1 Movement of the rightmost eigenvalues w.r.t. the hydrodynamic resistance R

Fig.8.2 Movement of the rightmost eigenvalues w.r.t. the cross-sectional area

Sensitivity Analysis

First, note that the characteristic equation of the system is

Differentiating both side of the characteristic equation with respect to the parameter A gives

Differentiating both side of the characteristic equation with respect to the parameter R gives

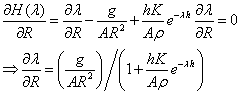
Since the rightmost eigenvalues of the nominal system is obtained as =  −0.2253 (see Ex.2.1),  one can substitute these values in the equations and obtain the sensitivity of the rightmost eigenvalues w.r.t. the parameters.

,

A positive sensitivity means that when the rightmost eigenvalue will further move to the right in the s-plane the parameter increases. This matches the results in Fig.8.1 and Fig.8.2 and further tells the size of the increments.

Example 8.2 Pendulum System

Consider feedback control problem in Ex. 5.2 for the linearized pendulum system:

where . The state feedback control is implemented assuming both states are measurable

Thus, the closed-loop system becomes

In this example, we will explore the relationship between the rightmost eigenvalues and the pendulum length l as well as the pendulum mass m for this second-order system. The nominal values of the parameters are the same as in Ex. 5.2 (l=2m, m=1kg, g=10ms^-2,  and h=0.2s).  The gains of the controller are selected as , which places the rightmost eigenvalues of the closed-loop system at (See Ex. 6.2 for more information if interested).

Rightmost Eigenvalue Analysis

First, calculate the rightmost eigenvalues of the closed-loop system with all nominal parameter values except m=(0.8:0.1:1.2)m_nom, where m_nom  is the nominal mass. As shown in Fig.8.3, the increase of m leads to the increase of the rightmost eignvalues in the s-plane, meaning an decreased stability of the system. Similarly, in Fig. 8.4, the rightmost eigenvalues move further to the right in the s-place as the length l increases.

Fig.8.3 Movement of the rightmost eigenvalues w.r.t. the mass m

Fig.8.4 Movement of the rightmost eigenvalues w.r.t. the length l

Sensitivity Analysis

First, calculate the characteristic equation of the system

Then, differentiate both side of the characteristic equation with respect to the parameter m

Similarly, differentiate both side of the characteristic equation with respect to the parameter l

The rightmost eigenvalues of the nominal system are =  . Note that here the rightmost eigenvalues are a pair complex conjugate numbers. One can use either of them to calculate the sensitivity. For example, substituting  gives

,

Thus, when m or l increases, the complex pole with positive imaginary part will be closer to the real axis and right-half plane.

If is used, it yields

,

, which leads to the same conclusion. These results from the sensitivity analysis coincide with the results shown in Fig.8.3 and Fig.8.4 and further quantify these relationships.