

 |
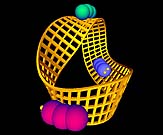 |
A simple endless band in the form of belt-shaped loop (below left) has two distinct surfaces and two edges. Moving from one surface to the opposite site requires crossing one of the edges.
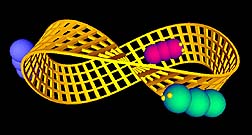
The Moebius Strip is an endless band that includes a half twist (below right). Amazingly, the band has only one surface and only one edge. Moving along the surface (like Escher's ants) will bring you to the opposite site without crossing the edge.
 simple endless band ( load VRML ) |
 endless band with half twist ( load VRML ) |
| Load the VRML Animation (11.0K) of the Moebius Strip |


|
|
Return to VRL Home Page http://www-VRL.umich.edu |
|
Return to Project Overview |