Runaway Reactions

Example: CSTR Runaway For Zero and First Order Reactions

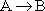
The isomerization reaction

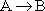
is carried out in a CSTR with a heat exchanger. We want to construct a stability diagram. First we will consider a zero order reaction with

Next, we will consider a first order reaction to be with

Construct the stability curves for a zero order reaction, (S₀), and a first order reaction, (S₁), as a function of T_C.

Additional Information

The ratio of inerts to A fed is 2 to 1.

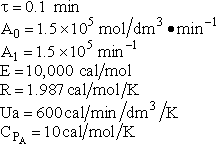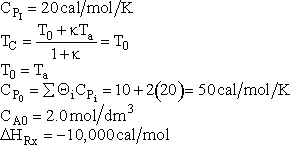Solution for Zero Order Reaction

(1)

Choose T_C and solve for T^* using the Polymath program in Table 1.

We shall use the same Polymath program shown in Table 1 to solve for S₀ and S₁. Note, in the Polymath program for this zero order reaction we let T₁ = T^* and then solve Equation (4) for T₁.

After solving for T₁ (i.e., T^*), we substitute for T₁ to find X^* in Equation (2) and then also into Equation (1) to find S₀ at the chosen T_C

We can calculate the conversion (X₁) in the Polymath program for this zero order reaction

Provided X₁ ≤ 1. Otherwise X₁ = 1. Choose another T_C and repeat solution (Equations (3) through (6)) to construct S₀ versus T_C in Table 2 which we will use to find regions of stability

Solution for First Order Reaction

Use Polymath to solve in Equation (7) for T^*

Note: In the Polymath program we let T^* ≡ T for a first order reaction

Evaluate X^* at this T_C

Calculate S₁ at this T_C

The Polymath solution for T_C = 475K is given below. We now choose another value of T_C and repeat to find T^* and then S₁ to construct a table of S₁ versus T_C as shown in Table 2.

Table 1

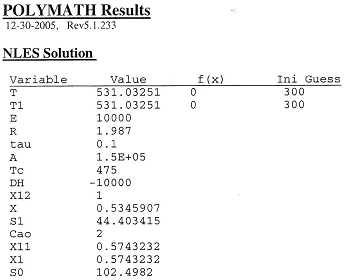
Table 2

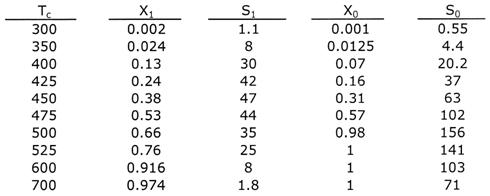
When this program is repeated for different values of T_C, Figure 1 can be developed using Table 2 where both S₀ and S₁ are plotted as a function of T_C on Figure 1.

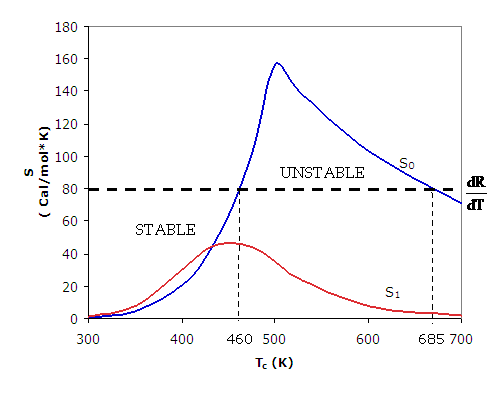
Figure 1. Stability plot.

We now can find the region of stability and of runaway

          Recall that

          then taking the derivative

          also recall

           When

runaway will NOT occur. However,

           when (i.e., )

runaway WILL occur.

           We see that for the first order reaction is globally stable for all T_C. However, we see the zero order reaction will run away when the entering temperature T_C is increased above 460K. We also note the runaway reaction becomes stable again as T_C is further increased to values above 685K.