4. Stoichiometry*


Rationale For Chapter 4

In chapter 2 we saw that if we had –rA as a function of X, [–rA= f(X)] we could size many reactors and reactor sequences and systems.

How do we obtain –rA = f(X)?

We do this in two steps

1. Part 1 - Chapter 3 Rate Law – Find the rate as a function of concentration,

          –rA = k fn (CA, CB …)

2. Part 2 - Chapter 4 Stoichiometry – Find the concentration as a function of conversion

          CA = g(X)

Combine Part 1 and Part 2 to get -rA=f(X)

Topics

Part 2: Stoichiometry
  1. Batch System Stoichiometric Table
  2. Flow System Stoichiometric Table

Stoichiometry

We shall set up Stoichiometric Tables using A as our basis of calculation in the following reaction. We will use the stoichiometric tables to express the concentration as a function of conversion. We will combine Ci = f(X) with the appropriate rate law to obtain -rA = f(X).



Batch System Stoichiometric Table (p.4-2) top

Species Symbol Initial Change Remaining
A A
B B
C C
D D
Inert I
________		 -------
____________

Where:

and


Concentration -- Batch System:


Constant Volume Batch:

Note:              if the reaction occurs in the liquid phase

                                               or 

         if a gas phase reaction occurs in a rigid (e.g., steel) batch reactor
Then
etc.
        

            if       then

            Constant Volume Batch

            and we have -ra=f(x)
 

Writing -rA soley as a function of X


Flow System Stoichiometric Table (p.4-9) top
Species Symbol Reactor Feed Change Reactor Effluent
A A
B B
C C
D D
Inert I
________		 -------
____________

Where:

and

Concentration -- Flow System:



Liquid Phase Flow System:


    Flow Liquid Phase

etc.

 

If the rate of reaction were -rA = kCACB then we would have

This gives us -rA = f(X). Consequently, we can use the methods discussed in Chapter 2 to size a large number of reactors, either alone or in series.

Gas Phase Flow System:

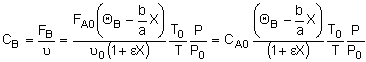etc.

Again, these equations give us information about -rA = f(X), which we can use to size reactors.


For example if the gas phase reaction has the rate law 

then 

     Flow Gas Phase

with


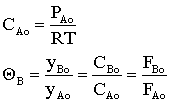
Rate Law in terms of Partial Pressures

Stoichiometry Table for Conversion

Oxidation of Naphthalene to Phtahalic Anhydride

Critical Thinking Questions for the Oxidation of Naphthalene

Production of Nitric Acid

Expressing a Catalytic Rate Law in Terms of Conversion

 

Calculating the equilibrium conversion for gas phase reaction

Consider the following elementary reaction with KC and = 20 dm3/mol and CA0 = 0.2 mol/dm3. Pure A fed. Calculate the equilibrium conversion, Xe, for both a batch reactor and a flow reactor.

Solution

At equilibrium

Stoichiometry

Batch

Species Initial Change Remaining
A NA0 -NA0X NA = NA0(1-X)
B 0 +NA0X/2 NB = NA0X/2
  NT0 = NA0   NT = NA0 - NA0X/2

Constant Volume V = V0

Solving

Flow

Species Fed Change Remaining
A FA0 -FA0X FA = F A0(1-X)
B 0 +FA0X/2 FB = F A0X/2
  FT0 = F A0   FT = F A0 - F A0X/2

  Recall

The following humorous video on limiting reactants was made by Professor Lane's 2008 Chemical Reaction Engineering class at the University of Alabama, Tuscaloosa.

You may access the video by connecting to the internet and clicking the image below

Old Exam Questions

Matching CA versus X curves
What is wrong with this solution?
Objective Assessment of Chapter 4
 

* All chapter references are for the 1st Edition of the text Essentials of Chemical Reaction Engineering .

top